已知抛物线的方程为
，直线
的方程为
，点
关于直线的对称点在抛物线上．
（1）求抛物线的方程；
（2）已知
，点
是抛物线的焦点，
是抛物线上的动点，求
的最小值及此时点的坐标；
（3）设点
、
是抛物线上的动点，点
是抛物线与
轴正半轴交点，
是以为直角顶点的直角三角形．试探究直线
是否经过定点？若经过，求出定点的坐标；若不经过，请说明理由．
已知矩阵A＝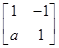
，若点P(1，1)在矩阵A对应的变换作用下得到点P′(0，-8)．
(1)求实数a的值；
(2)求矩阵A的特征值．
二阶矩阵M对应的变换将点(1，－1)与(－2，1)分别变换成点(－1，－1)与(0，－2)．
(1)求矩阵M；
(2)设直线l在变换M作用下得到了直线m：x－y＝4，求l的方程．
二阶矩阵M对应的变换将点(1，－1)与(－2，1)分别变换成点(－1，－1)与(0，－2)．设直线l在变换M作用下得到了直线m：2x－y＝4，求l的方程．
已知矩阵M＝
，向量α＝
，β＝
.
(1)求向量3α＋
β在TM作用下的象；
(2)求向量4Mα－5Mβ.
如图所示，四边形ABCD和四边形AB′C′D分别是矩形和平行四边形，其中各点的坐标分别为A(－1，2)、B(3，2)、C(3，－2)、D(－1，－2)、B′(3，7)、C′(3，3)．求将四边形ABCD变成四边形AB′C′D的变换矩阵M.