为了了解高一年级学生的身高情况,某校按10%的比例对全校800名高一年级学生按性别进行抽样检查,得到如下频数分布表:
表1:男生身高频数分布表
| 身高(cm) |
[160,165) |
[165,170) |
[170,175) |
[175,180) |
[180,185) |
[185,190] |
| 频数 |
2 |
5 |
14 |
13 |
4 |
2 |
表2:男生身高频数分布表
| 身高(cm) |
[150,155) |
[150,160) |
[160,165) |
[165,170) |
[170,175) |
[175,180] |
| 频数 |
2 |
12 |
16 |
6 |
3 |
1 |
(1)分别估计高一年级男生和女生的平均身高;
(2)在样本中,从身高180cm以上的男生中任选2人,求至少有一人身高在185cm以上的概率.
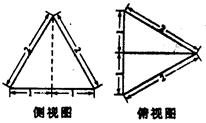
三棱锥 及其侧视图、俯视图如图所示。设
及其侧视图、俯视图如图所示。设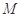 ,
,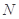 分别为线段
分别为线段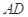 ,
,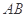 的中点,
的中点,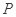 为线段
为线段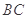 上的点,且
上的点,且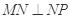 。
。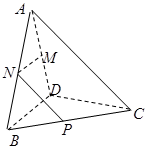
(1)证明: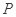 为线段
为线段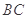 的中点;
的中点;
(2)求二面角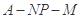 的余弦值。
的余弦值。
如图,在四棱柱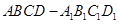 中,底面
中,底面 是等腰梯形,
是等腰梯形,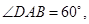
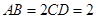 ,
,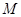 是线段
是线段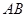 的中点.
的中点.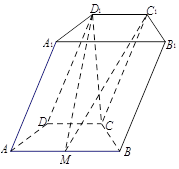
(Ⅰ)求证: ;
;
(Ⅱ)若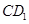 垂直于平面
垂直于平面 且
且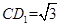 ,求平面
,求平面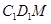 和平面
和平面 所成的角(锐角)的余弦值.
所成的角(锐角)的余弦值.
如图,三棱柱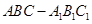 中,点
中,点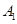 在平面ABC内的射影D在AC上,
在平面ABC内的射影D在AC上,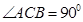 ,
,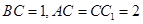 .
.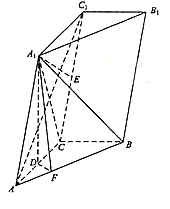
(1)证明: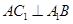 ;
;
(2)设直线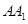 与平面
与平面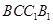 的距离为
的距离为 ,求二面角
,求二面角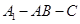 的大小.
的大小.
如图,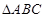 和
和 所在平面互相垂直,且
所在平面互相垂直,且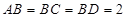 ,
, ,E、F分别为AC、DC的中点.
,E、F分别为AC、DC的中点.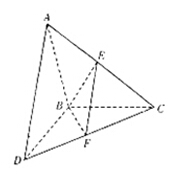
(1)求证: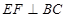 ;
;
(2)求二面角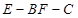 的正弦值.
的正弦值.
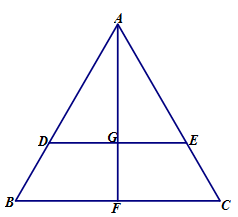
如图,在边长为1的等边三角形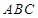 中,
中,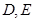 分别是
分别是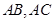 边上的点,
边上的点,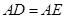 ,
,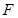 是
是 的中点,
的中点,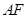 与
与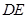 交于点
交于点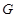 ,将
,将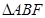 沿
沿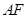 折起,得到如图所示的三棱锥
折起,得到如图所示的三棱锥 ,其中
,其中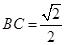 .
.
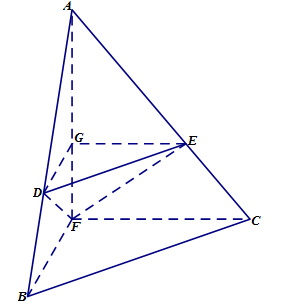
(1)证明: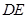 //平面
//平面 ;
;
(2)证明: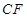
 平面
平面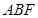 ;
;
(3)当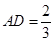 时,求三棱锥
时,求三棱锥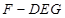 的体积
的体积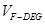 .
.