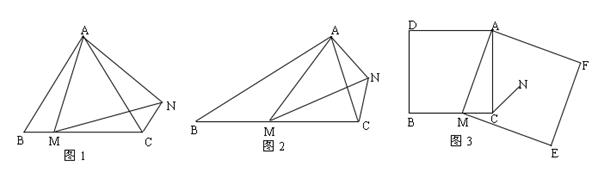
如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.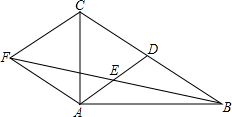
国家环保局统一规定,空气质量分为5级.当空气污染指数达0—50时为1级,质量为优;51—100时为2级,质量为良;101—200时为3级,轻度污染;201—300时为4级,中度污染;300以上时为5级,重度污染.某城市随机抽取了2015年某些天的空气质量检测结果,并整理绘制成如下两幅不完整的统计图.请根据图中信息,解答下列各题: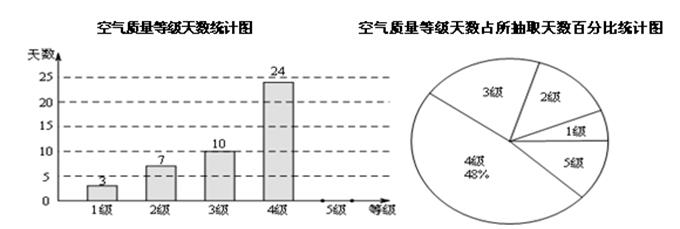
(1)本次调查共抽取了_______天的空气质量检测结果进行统计;
(2)补全条形统计图;
(3)扇形统计图中3级空气质量所对应的圆心角为________°;
(4)如果空气污染达到中度污染或者以上,将不适宜进行户外活动,根据目前的统计,请你估计2015年该城市有多少天不适宜开展户外活动.(2015年共365天)
先化简分式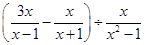 ,再取一个合适的值代入,求原分式的值。
,再取一个合适的值代入,求原分式的值。
(1)计算: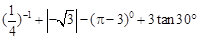
(2)解不等式组: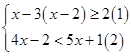
如图,抛物线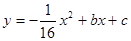 经过△ABC的三个顶点,点A坐标为(0,6),点C坐标为(4,6),点B在x轴正半轴上.
经过△ABC的三个顶点,点A坐标为(0,6),点C坐标为(4,6),点B在x轴正半轴上.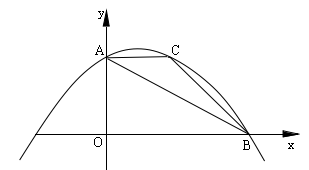
(1)求该抛物线的函数表达式和点B的坐标.
(2)将经过点B、C的直线平移后与抛物线交于点M,与x轴交于点N,当以B、C、M、N为顶点的四边形是平行四边形时,请求出点M的坐标.
(3)①动点D从点O开始沿线段OB向点B运动,同时以OD为边在第一象限作正方形ODEF,当正方形的顶点E恰好落在线段AB上时,则此时正方形的边长为.
②将①中的正方形ODEF沿OB向右平移,记平移中的正方形ODEF为正方形O′D′E′F′,当点D与点B重合时停止平移.设平移的距离为x,在平移过程中,设正方形O′D′E′F′与△ABC重叠部分的面积为y,请你画出相对应的图形并直接写出y与x之间的函数关系式.
某数学活动小组在一次活动中,对一个数学问题作如下探究:
【问题发现】如图1,在等边三角形ABC中,点M是边BC上任意一点,连接AM,以AM为边作等边三角形AMN,连接CN,证明:BM=CN.
【变式探究】如图2,在等腰三角形ABC中,BA=BC,∠ABC=∠α,点M为边BC上任意一点,以AM为腰作等腰三角形AMN,MA=MN,使∠AMN=∠ABC,连接CN,请求出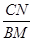 的值.
的值.
(用含α的式子表示出来)
【解决问题】如图3,在正方形ADBC中,点M为边BC上一点,以AM为边作正方形作AMEF,N为正方形AMEF的中心,连接CN,若正方形AMEF的边长为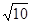 ,CN=
,CN= ,请你求正方形ADBC的边长.
,请你求正方形ADBC的边长.