如图,直三棱柱 的底面
的底面 是等腰直角三角形,
是等腰直角三角形, ,侧棱
,侧棱 底面
底面 ,且
,且 ,
, 是
是 的中点.
的中点.
(1)求直三棱柱 的全面积;
的全面积;
(2)求异面直线 与
与 所成角
所成角 的大小(结果用反三角函数表示);
的大小(结果用反三角函数表示);
(本小题满分12分)已知 为等差数列
为等差数列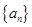 的前
的前 项和,
项和, ,
, .
.
(Ⅰ)求数列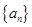 的通项公式;
的通项公式;
(Ⅱ)若数列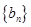 满足:
满足: ,求数列
,求数列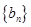 的前
的前 项和
项和 .
.
(本小题满分12分)如图,在四棱锥 中,
中,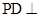 平面
平面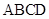 ,
,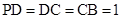 ,
,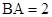 ,
,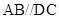 ,
, ,点
,点 、
、 、
、 分别是线段
分别是线段 、
、 、
、 的中点.
的中点.
(Ⅰ)求证: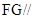 平面
平面 ;
;
(Ⅱ)求证: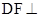 平面
平面 .
.
(本小题满分12分)山东省济南市为了共享优质教育资源,实现名师交流,甲、乙两校各有 名教师报名交流,其中甲校
名教师报名交流,其中甲校 男
男 女,乙校
女,乙校 男
男 女.
女.
(Ⅰ)若从甲校和乙校报名的教师中各任选 名,写出所有可能的结果,并求选出的
名,写出所有可能的结果,并求选出的 名教师性别相同的概率;
名教师性别相同的概率;
(Ⅱ)若从报名的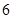 名教师中任选
名教师中任选 名,写出所有可能的结果,并求选出的
名,写出所有可能的结果,并求选出的 名教师来自同一学校的概率.
名教师来自同一学校的概率.
(本小题满分12分)在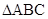 中,
中, ,
, ,
, 分别是角
分别是角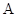 ,
, ,
,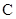 的对边,且
的对边,且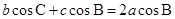 .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若函数 ,
,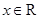 .
.
(1)求函数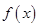 的最小正周期;
的最小正周期;
(2)求函数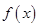 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
(本小题满分14分)已知函数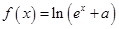 (
( 为常数,
为常数, 为自然对数的底数)是实数集
为自然对数的底数)是实数集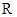 上的奇函数,函数
上的奇函数,函数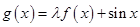 在区间
在区间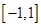 上是减函数.
上是减函数.
(1)求实数 的值;
的值;
(2)若 在
在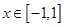 上恒成立,求实数
上恒成立,求实数 的取值范围;
的取值范围;
(3)讨论关于 的方程
的方程 的根的个数.
的根的个数.