如图,在四棱锥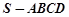 中,底面
中,底面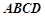 是直角梯形,
是直角梯形,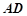 ∥
∥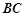 ,
,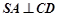 ,
, ⊥平面SAD,点
⊥平面SAD,点 是
是 的中点,且
的中点,且 ,
, .
. 
(1)求四棱锥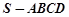 的体积;
的体积;
(2)求证: ∥平面
∥平面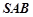 ;
;
(3)求直线 和平面
和平面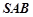 所成的角的正弦值.
所成的角的正弦值.
某研究性学习小组对昼夜温差与某种子发芽数的关系进行研究,他们分别记录了四天中每天昼夜温差与每天100粒种子浸泡后的发芽数,得到如下资料:
| 时间 |
第一天 |
第二天 |
第三天 |
第四天 |
| 温差(℃) |
9 |
10 |
8 |
11 |
| 发芽数(粒) |
33 |
39 |
26 |
46 |
(1)求这四天浸泡种子的平均发芽率;
(2)若研究的一个项目在这四天中任选2天的种子发芽数来进行,记发芽的种子数分别为m,n(m<n),则以(m,n)的形式列出所有的基本事件,并求“m,n满足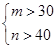 ”的事件A的概率.
”的事件A的概率.
已知向量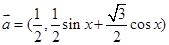 与
与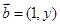 共线,设函数
共线,设函数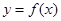 .
.
(1)求函数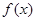 的周期及最大值;
的周期及最大值;
(2)已知锐角 △ABC 中的三个内角分别为 A、B、C,若有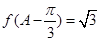 ,边 BC=
,边 BC=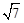 ,
,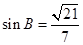 ,求 △ABC 的面积.
,求 △ABC 的面积.
已知函数y=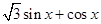
(Ⅰ)求函数y的最小正周期;
(Ⅱ)求函数y的最大值.
已知等差数列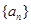 中,
中,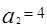 ,其前n项和
,其前n项和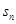 满足
满足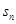 =
=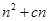
(1)求实数c的值
(2)求数列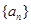 的通项公式
的通项公式