在直角坐标系 中,直线
中,直线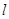 的参数方程为
的参数方程为 (
(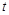 为参数),若以直角坐标系
为参数),若以直角坐标系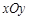 的
的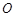 点为极点,
点为极点,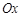 为极轴,且长度单位相同,建立极坐标系,得曲线
为极轴,且长度单位相同,建立极坐标系,得曲线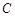 的极坐标方程为
的极坐标方程为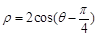 .
.
(1)求直线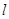 的倾斜角;
的倾斜角;
(2)若直线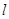 与曲线
与曲线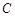 交于
交于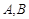 两点,求
两点,求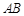
已知矩阵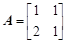 ,向量
,向量 .求向量
.求向量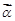 ,使得
,使得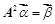 .
.
已知数列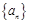 单调递增,且各项非负,对于正整数
单调递增,且各项非负,对于正整数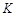 ,若任意的
,若任意的 ,
, (
(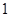 ≤
≤ ≤
≤ ≤
≤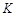 ),
), 仍是
仍是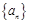 中的项,则称数列
中的项,则称数列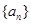 为“
为“ 项可减数列”.
项可减数列”.
(1)已知数列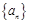 是首项为2,公比为2的等比数列,且数列
是首项为2,公比为2的等比数列,且数列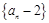 是“
是“ 项可减数
项可减数
列”,试确定 的最大值;
的最大值;
(2)求证:若数列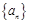 是“
是“ 项可减数列”,则其前
项可减数列”,则其前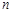 项的和
项的和 ;
;
(3)已知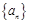 是各项非负的递增数列,写出(2)的逆命题,判断该逆命题的真假,
是各项非负的递增数列,写出(2)的逆命题,判断该逆命题的真假,
并说明理由.
已知函数 (
( ).
).
(1)若 ,
, 在
在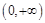 上是单调增函数,求
上是单调增函数,求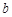 的取值范围;
的取值范围;
(2)若 ,求方程
,求方程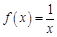 在
在 上解的个数.
上解的个数.
已知椭圆 的右焦点为
的右焦点为 ,点
,点 在圆
在圆 上任意一点(点
上任意一点(点 第一象限内),过点
第一象限内),过点 作圆
作圆 的切线交椭圆
的切线交椭圆 于两点
于两点 、
、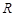 .
.
(1)证明: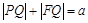 ;
;
(2)若椭圆离心率为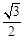 ,求线段
,求线段 长度的最大值.
长度的最大值.