已知函数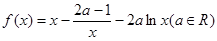 .
.
(1)若函数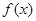 在
在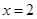 时取得极值,求实数
时取得极值,求实数 的值;
的值;
(2)若 对任意
对任意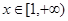 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
双曲线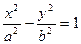 (a>1,b>0)的焦距为2c,直线l过点(a,0)和(0,b),且点(1,0)到直线l的距离与点(-1,0)到直线l的距离之和s≥
(a>1,b>0)的焦距为2c,直线l过点(a,0)和(0,b),且点(1,0)到直线l的距离与点(-1,0)到直线l的距离之和s≥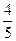 c.求双曲线的离心率e的取值范围.
c.求双曲线的离心率e的取值范围.
如图椭圆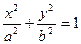 (a>b>0)的上顶点为A,左顶点为B, F为右焦点, 过F作平行与AB的直线交椭圆于C、D两点. 作平行四边形OCED, E恰在椭圆上.
(a>b>0)的上顶点为A,左顶点为B, F为右焦点, 过F作平行与AB的直线交椭圆于C、D两点. 作平行四边形OCED, E恰在椭圆上.
(1)求椭圆的离心率;
(2)若平行四边形OCED的面积为 , 求椭圆方程.
, 求椭圆方程.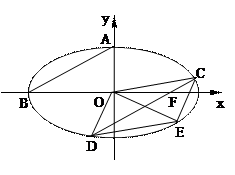
已知复数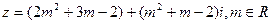
根据下列条件,求m值.
(1)z是实数;(2)z是虚线;(3)z是纯虚数;(4)z=0.
求证:关于x的方程x2+2ax+b="0" 有实数根,且两根均小于2的充分但不必要条件是a≥2且|b| ≤4.
给定两个命题, :对任意实数
:对任意实数 都有
都有 恒成立;
恒成立; :关于
:关于 的方程
的方程 有实数根;如果
有实数根;如果 与
与 中有且仅有一个为真命题,求实数
中有且仅有一个为真命题,求实数 的取值范围
的取值范围