以下茎叶图记录了甲、乙两组各四名同学的植树棵数。乙组记录中有一个数据模糊,无法确认,在图中经X表示。
(1)如果X=8,求乙组同学植树棵数的平均数和方差
(2)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数为19的概率
设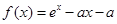 .
.
(Ⅰ)若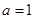 ,求
,求 的单调区间;
的单调区间;
(Ⅱ) 若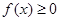 对一切
对一切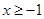 恒成立,求
恒成立,求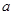 的取值范围.
的取值范围.
如图,三棱柱ABC—A1B1C1的侧棱AA1⊥底面ABC,∠ACB = 90°,E是棱CC1上中点,F是AB中点,AC = 1,BC = 2,AA1 = 4.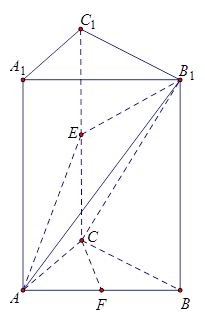
(1)求证:CF∥平面AEB1;(2)求三棱锥C-AB1E的体积.
设函数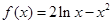 .(I)求函数
.(I)求函数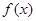 的单调递增区间;
的单调递增区间;
(II) 若关于 的方程
的方程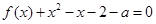 在区间
在区间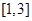 内恰有两个不同的实根,求实数
内恰有两个不同的实根,求实数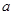 的取值范围.
的取值范围.
已知函数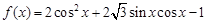 .
.
(Ⅰ)求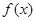 的最小正周期;
的最小正周期;
(Ⅱ)在△ABC中,角A,B,C所对的边分别是 ,若
,若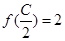 且
且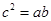 ,
,
试判断△ABC的形状.
省少年篮球队要从甲、乙两所体校选拔队员。现将这两所体校共20名学生的身高绘制成如下茎叶图(单位:cm):若身高在180cm以上(包括180cm)定义为“高个子”,身高在180cm以下(不包括180cm)定义为“非高个子”.
(1)用分层抽样的方法从“高个子”和“非高个子”中抽取5人,如果从这5人中随
机选2人,那么至少有一人是“高个子”的概率是多少?
(2)从两队的“高个子”中各随机抽取1人,求恰有1人身高达到190cm的概率.