(本小题满分14分)
已知二次函数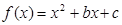 的图象过点
的图象过点 ,且函数对称轴方程为
,且函数对称轴方程为 .
.
(Ⅰ)求函数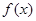 的解析式;
的解析式;
(Ⅱ)设函数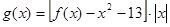 ,求
,求 在区间
在区间 上的最小值
上的最小值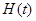 ;
;
(Ⅲ)探究:函数 的图象上是否存在这样的点,使它的横坐标是正整数,纵坐标是一个完全平方数?如果存在,求出这样的点的坐标;如果不存在,请说明理由.
的图象上是否存在这样的点,使它的横坐标是正整数,纵坐标是一个完全平方数?如果存在,求出这样的点的坐标;如果不存在,请说明理由.
已知点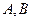 分别是射线
分别是射线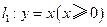 ,
,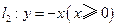 上的动点,
上的动点,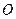 为坐标原点,且
为坐标原点,且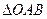 的面积为定值2.
的面积为定值2.
(I)求线段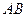 中点
中点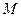 的轨迹
的轨迹 的方程;
的方程;
(II)过点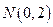 作直线
作直线 ,与曲线
,与曲线 交于不同的两点
交于不同的两点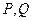 ,与射线
,与射线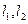 分别交于点
分别交于点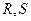 ,若点
,若点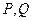 恰为线段
恰为线段 的两个三等分点,求此时直线
的两个三等分点,求此时直线 的方程.
的方程.
已知双曲线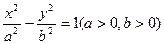 的一条渐近线方程为
的一条渐近线方程为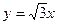 ,两条准线的距离为l.
,两条准线的距离为l.
(1)求双曲线的方程;
(2)直线l过坐标原点O且和双曲线交于两点M、N,点P为双曲线上异于M、N的一点,且直线PM,PN的斜率均存在,求kPM·kPN的值.
已知定圆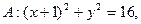 圆心为A,动圆M过点B(1,0)且和圆A相切,动圆的圆心M的轨迹记为C.
圆心为A,动圆M过点B(1,0)且和圆A相切,动圆的圆心M的轨迹记为C.
(I)求曲线C的方程;
(II)若点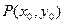 为曲线C上一点,求证:直线
为曲线C上一点,求证:直线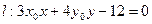 与曲线C有且只有一个交点.
与曲线C有且只有一个交点.
已知抛物线 ,点P(1,-1)在抛物线C上,过点P作斜率为k1、k2的两条直线,分别交抛物线C于异于点P的两点A(x1,y1),B(x2,y2),且满足k1+k2=0.
,点P(1,-1)在抛物线C上,过点P作斜率为k1、k2的两条直线,分别交抛物线C于异于点P的两点A(x1,y1),B(x2,y2),且满足k1+k2=0.
(I)求抛物线C的焦点坐标;
(II)若点M满足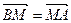 ,求点M的轨迹方程.
,求点M的轨迹方程.
已知椭圆W的中心在原点,焦点在 轴上,离心率为
轴上,离心率为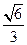 ,两条准线间的距离为6. 椭圆W的左焦点为
,两条准线间的距离为6. 椭圆W的左焦点为 ,过左准线与
,过左准线与 轴的交点
轴的交点 任作一条斜率不为零的直线
任作一条斜率不为零的直线 与椭圆W交于不同的两点
与椭圆W交于不同的两点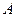 、
、 ,点
,点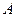 关于
关于 轴的对称点为
轴的对称点为 .
.
(Ⅰ)求椭圆W的方程;
(Ⅱ)求证: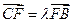 (
(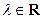 );
);
(Ⅲ)求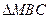 面积
面积 的最大值.
的最大值.