已知抛物线 ,点P(1,-1)在抛物线C上,过点P作斜率为k1、k2的两条直线,分别交抛物线C于异于点P的两点A(x1,y1),B(x2,y2),且满足k1+k2=0.
,点P(1,-1)在抛物线C上,过点P作斜率为k1、k2的两条直线,分别交抛物线C于异于点P的两点A(x1,y1),B(x2,y2),且满足k1+k2=0.
(I)求抛物线C的焦点坐标;
(II)若点M满足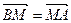 ,求点M的轨迹方程.
,求点M的轨迹方程.
(1)当 为何值时,直线
为何值时,直线 与直线
与直线 平行?
平行?
(2)当 为何值时,直线
为何值时,直线 与直线
与直线 垂直?
垂直?
已知数列 的前
的前 项和为
项和为 ,数列
,数列 满足
满足
 (
( ).
).
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的通项公式;
的通项公式;
(3)求 的值.
的值.
已知甲船正在大海上航行,当它位于A处时获悉,在其正东方向相距20海里的B处有一艘渔船遇险等待营救,甲船立即以10海里/小时的速度匀速前往救援,同时把消息告知在甲船的南偏西 ,相距10海里C处的乙船,乙船当即决定匀速前往救援,并且与甲船同时到达。(供参考使用:
,相距10海里C处的乙船,乙船当即决定匀速前往救援,并且与甲船同时到达。(供参考使用: ).
).
(1)试问乙船航行速度的大小;
(2)试问乙船航行的方向(试用方位角表示,如北偏东…度).
已知 为等差数列
为等差数列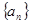 的前
的前 项和,
项和, .
.
⑴求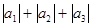 ;
;
⑵求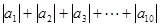 ;
;
⑶求 .
.
在△ 中,内角
中,内角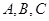 的对边分别为
的对边分别为 ,且
,且 .
.
(1)求角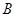 的值;
的值;
(2)若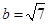 ,
,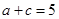 ,求
,求 的面积.
的面积.