甲、乙、丙三人参加了一家公司的招聘面试,面试合格者可正式签约.甲表示只要面试合格就签约.乙、丙则约定:两人面试都合格就一同签约,否则两人都不签约.设每人面试合格的概率都是 , 且面试是否合格互不影响.
求: ( I ) 至少有 1 人面试合格的概率;
( II ) 签约人数 的分布列和数学期望.
如图,已知平行四边形 和矩形
和矩形 所在的平面互相垂直,
所在的平面互相垂直, ,
,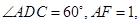
 是线段
是线段 的中点.
的中点.
(Ⅰ)求二面角 的正弦值;
的正弦值;
(Ⅱ)设点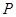 为一动点,若点
为一动点,若点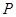 从
从 出发,沿棱按照
出发,沿棱按照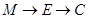 的路线运动到点
的路线运动到点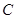 ,求这一过程中形成的三棱锥
,求这一过程中形成的三棱锥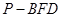 的体积的最小值.
的体积的最小值.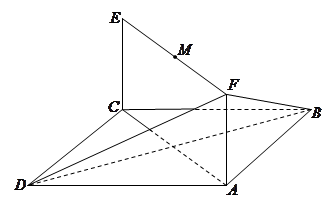
在直角坐标平面上有一点列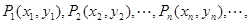 对一切正整数n,点
对一切正整数n,点 在函数
在函数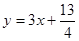 的图象上,且
的图象上,且 的横坐标构成以
的横坐标构成以 为首项,-1为公差的等差数列
为首项,-1为公差的等差数列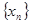 .
.
(Ⅰ)求点 的坐标;
的坐标;
(Ⅱ)设抛物线列C1,C2,C3,…,Cn,…中的每一条的对称轴都垂直于x轴,抛物线Cn的顶点为Pn,且过点Dn(0, ).记与抛物线Cn相切于点Dn的直线的斜率为kn,求
).记与抛物线Cn相切于点Dn的直线的斜率为kn,求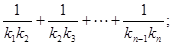
已知函数 .
.
(Ⅰ)求函数 的最小正周期和值域;
的最小正周期和值域;
(Ⅱ)若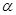 为第二象限角,且
为第二象限角,且 ,求
,求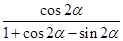 的值.
的值.
已知函数f(x)=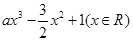 ,其中a>0.
,其中a>0.
(Ⅰ)若a=1,求曲线y=f(x)在点(2,f(2))处的切线方程;
(Ⅱ)若在区间 上,f(x)>0恒成立,求a的取值范围.
上,f(x)>0恒成立,求a的取值范围.
已知椭圆C: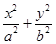 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为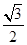 ,且在x轴上的顶点分别为
,且在x轴上的顶点分别为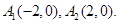
(1)求椭圆方程;
(2)若直线 :
: 与
与 轴交于点T,P为
轴交于点T,P为 上异于T的任一点,直线
上异于T的任一点,直线 分别与椭圆交于M、N两点,试问直线MN是否通过椭圆的焦点?并证明你的结论.
分别与椭圆交于M、N两点,试问直线MN是否通过椭圆的焦点?并证明你的结论.