已知椭圆C1和抛物线C2有公共焦点F(1，0)，C1的中心和C2的顶点都在坐标原点，过点M(4，0)的直线l与抛物线C2分别相交于A ，B两点．
(1)如图所示，若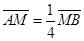
，求直线l的方程；
(2)若坐标原点O关于直线l的对称点P在抛物线C2上，直线l与椭圆C1有公共点，求椭圆C1的长轴长的最小值．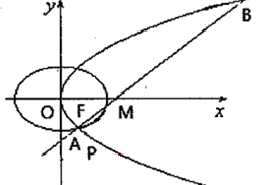
某乡镇现在人均一年占有粮食360千克，如果该乡镇人口平均每年增长1.2%，粮食总产量平均每年增长4%，那么
年后若人均一年占有
千克粮食，求出函数关于的解析式。
按复利计算利息的一种储蓄，本金为
元，每期利率为
，设本利和为
，存期为
，写出本利和随存期变化的函数式，如果存入本金1000元，每期利率2.25%，试计算5期后的本利和是多少？
某渔场养鱼，鱼的重量增长率第一年为400%，以后每年重量增长率都是前一年的三分之一。同时鱼每年要损失预计重量的10%。预计养鱼的费用第一年是鱼苗成本的20%，以后每年的费用M（t）与年数t满足关系式
（其中
为鱼苗成本，
）。问该渔场的鱼养几年后全部捕捞，鱼的产值高且费用较少（设鱼苗价30元/斤，成鱼市场价7元/斤）。
铁道机车运行1小时所需的成本由两部分组成，固定部分为
元，变动部分与运行速度V（千米/小时）的平方成正比。比例系数为k（k≠0）。如果机车匀速从甲站开往乙站，为使成本最省应以怎样的速度运行？
某市1994年底人口为20万，人均住房面积为8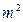
，计划1998年底人均住房面积达10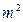。如果该市每年人口平均增长率控制在1%，要实现上述计划，这个城市每年平均至少要新增住房面积多少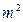万（结果以万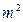为单位，保留两位小数）。