(本小题满分12分)已知椭圆C: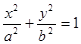 (a>b>0)与y轴的交点为A,B(点A位于点B的上方),F为左焦点,原点O到直线FA的距离为
(a>b>0)与y轴的交点为A,B(点A位于点B的上方),F为左焦点,原点O到直线FA的距离为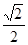 b.
b.
(Ⅰ)求椭圆C的离心率;
(Ⅱ)设b=2,直线y=kx+4与椭圆C交于不同的两点M,N,求证:直线BM与直线AN的交点G在定直线上.
已知 .
.
(1)求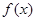 的最小正周期及
的最小正周期及 ;
;
(2)求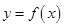 的单调增区间;
的单调增区间;
(3)当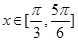 时,求
时,求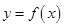 的值域.
的值域.
已知 ,
, .
.
(1)求 及
及 ;
;
(2)求 的值.
的值.
已知二次函数 .
.
(1)若 ,试判断函数
,试判断函数 零点个数.
零点个数.
(2)若对 且
且 ,
, ,证明方程
,证明方程 必有一个实数根属于
必有一个实数根属于 .
.
(3)是否存在 ,使
,使 同时满足以下条件①当
同时满足以下条件①当 时,函数
时,函数 有最小值0;②对任意实数x,都有
有最小值0;②对任意实数x,都有 .若存在,求出
.若存在,求出 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
已知圆 :
: ,直线
,直线 过定点
过定点 .
.
(1)若直线 与圆相切,切点为
与圆相切,切点为 ,求线段
,求线段 的长度;
的长度;
(2)若 与圆相交于
与圆相交于 两点,线段
两点,线段 的中点为
的中点为 ,又
,又 与
与 :
: 的交点为
的交点为 ,判断
,判断 •
• 是否为定值,若是,则求出定值;若不是,请说明理由.
是否为定值,若是,则求出定值;若不是,请说明理由.
如图,正方形 的边长为1,正方形
的边长为1,正方形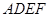 所在平面与平面
所在平面与平面 互相垂直,
互相垂直,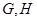 是
是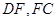 的中点.
的中点.
(1)求证: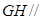 平面
平面 ;
;
(2)求证: ;
;
(3)求三棱锥 的体积.
的体积.