某书商为提高某套丛书的销量,准备举办一场展销会.据市场调查,当每套丛书售价定为x元时,销售量可达到15—0.1x万套.现出版社为配合该书商的活动,决定进行价格改革,将每套丛书的供货价格分成固定价格和浮动价格两部分,其中固定价格为30元,浮动价格(单位:元)与销售量(单位:万套)成反比,比例系数为10.假设不计其他成本,即销售每套丛书的利润=售价-供货价格.问:
(1)每套丛书售价定为100元时,书商能获得的总利润是多少万元?
(2)每套丛书售价定为多少元时,单套丛书的利润最大?
已知数列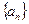 中,
中,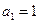 且
且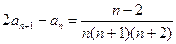 .
.
(I)设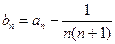 ,求数列
,求数列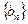 的通项公式;
的通项公式;
(II)设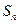 为数列
为数列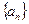 的前
的前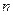 项和,求证:
项和,求证: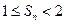 .
.
如图,四棱锥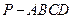 中,底面
中,底面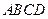 是平行四边形,
是平行四边形,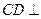 侧面
侧面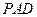 ,点
,点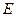 在侧棱
在侧棱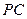 上,且
上,且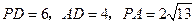 .
.
(Ⅰ)求证:平面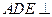 平面
平面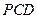 ;
;
(Ⅱ) 若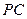 与
与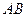 所成角为
所成角为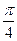 ,二面角
,二面角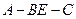 的大小为
的大小为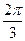 ,求
,求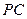 与平面
与平面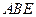 所成角的大小.
所成角的大小.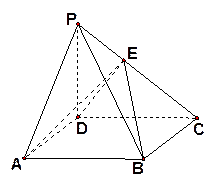
甲,乙两个同学同时报名参加某重点高校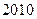 年自主招生,高考前自主招生的程序为审核材料和文化测试,只有审核过关后才能参加文化测试,文化测试合格者即可获得自主招生入选资格.已知甲,乙两人审核过关的概率分别为
年自主招生,高考前自主招生的程序为审核材料和文化测试,只有审核过关后才能参加文化测试,文化测试合格者即可获得自主招生入选资格.已知甲,乙两人审核过关的概率分别为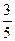 ,
,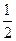 ,审核过关后,甲,乙两人文化测试合格的概率分别为
,审核过关后,甲,乙两人文化测试合格的概率分别为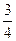 ,
,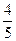 .
.
(Ⅰ)求甲,乙两人至少有一人通过审核的概率;
(Ⅱ) 设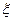 表示甲,乙两人中获得自主招生入选资格的人数,求
表示甲,乙两人中获得自主招生入选资格的人数,求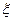 的数学期望.
的数学期望.
已知函数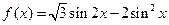 .
.
(Ⅰ)求函数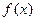 的单调减区间;
的单调减区间;
(Ⅱ)求使函数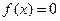 的
的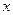 的集合.
的集合.
(本小题满分14分)20. 设函数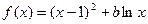 ,其中
,其中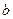 为常数.
为常数.
(1)当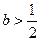 时,判断函数
时,判断函数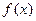 在定义域上的单调性;
在定义域上的单调性;
(2)若函数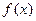 的有极值点,求
的有极值点,求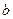 的取值范围及
的取值范围及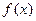 的极值点;
的极值点;
(3)求证对任意不小于3的正整数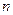 ,不等式
,不等式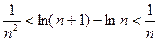 都成立.
都成立.