已知 为坐标原点,
为坐标原点, =(
=(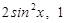 ),
), =(1,
=(1,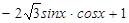 ),
),  .
.
(1)若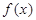 的定义域为[-
的定义域为[-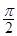 ,
, ],求y=
],求y=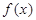 的单调递增区间;
的单调递增区间;
(2)若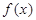 的定义域为[
的定义域为[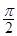 ,
, ],值域为[2,5],求
],值域为[2,5],求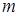 的值.
的值.
已知二次函数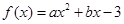 在
在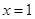 处取得极值,且在
处取得极值,且在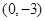 点处的切线与直线
点处的切线与直线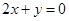 平行.
平行.
(1)求 的解析式;
的解析式;
(2)求函数 的单调递增区间及极值。
的单调递增区间及极值。
(3)求函数 在
在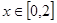 的最值。
的最值。
有9本不同的课外书,分给甲、乙、丙三名同学,求在下列条件下,各有多少种分法?
(1)甲得4本,乙得3本,丙得2本;
(2)一人得4本,一人得3本,一人得2本;
(3)甲、乙、丙各得3本.
已知复数z=(2+i)m2--2(1-i).当实数m取什么值时,复数z是:
(1)虚数;(2)纯虚数;(3)复平面内第二、四象限角平分线上的点对应的复数?
已知函数 .
.
(1)试判断函数 的单调性;
的单调性;
(2)设 ,求
,求 在
在 上的最大值;
上的最大值;
(3)试证明:对 ,不等式
,不等式 .
.
某大学生在开学季准备销售一种文具套盒进行试创业,在一个开学季内,每售出1盒该产品获利润50元,未售出的产品,每盒亏损30元.根据历史资料,得到开学季市场需求量的频率分布直方图,如下图所示.该同学为这个开学季购进了160盒该产品,以X(单位:盒,100≤X≤200)表示这个开学季内的市场需求量,Y(单位:元)表示这个开学季内经销该产品的利润.
(1)根据直方图估计这个开学季内市场需求量X的平均数和众数;
(2)将Y表示为X的函数;
(3)根据直方图估计利润不少于4800元的概率.