某村庄拟修建一个无盖的圆柱形蓄水池(不计厚度).设该蓄水池的底面半径为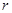 米,高为
米,高为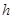 米,体积为
米,体积为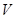 立方米.假设建造成本仅与表面积有关,侧面积的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为
立方米.假设建造成本仅与表面积有关,侧面积的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为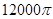 元(
元(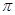 为圆周率).
为圆周率).
(1)将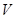 表示成
表示成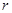 的函数
的函数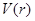 ,并求该函数的定义域;
,并求该函数的定义域;
(2)讨论函数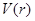 的单调性,并确定
的单调性,并确定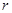 和
和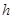 为何值时该蓄水池的体积最大.
为何值时该蓄水池的体积最大.
(本小题满分13分)
如图是两个独立的转盘(A)、(B),在两个图中三个扇形区域的圆心角分别为 ,用这两个转盘进行游戏,规则是:同时转动两个转盘待指针停下(当两个转盘中任意一个指针恰好落在分界线时,则这次转动无效,重新开始),记转盘(A)指针所对的区域为x,转盘(B)指针所对的区域为y,
,用这两个转盘进行游戏,规则是:同时转动两个转盘待指针停下(当两个转盘中任意一个指针恰好落在分界线时,则这次转动无效,重新开始),记转盘(A)指针所对的区域为x,转盘(B)指针所对的区域为y, ,设
,设 的值为
的值为

(1)求 的概率;
的概率;
(2)求随机变量 的发布列与数学期望。
的发布列与数学期望。
(本小题满分13分)
在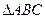 中,边a,b,c分别为角A,B,C的对边,若
中,边a,b,c分别为角A,B,C的对边,若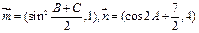 ,且
,且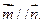
(1)求角A的大小;
(2)若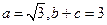 ,求
,求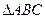 的面积S。
的面积S。
本小题满分12分)
古代印度婆罗门教寺庙内的僧侣们曾经玩过一种被称为“河内宝塔问题”的游戏,其玩法如下:如图,设有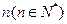 个圆盘依其半径大小,大的在下,小的在上套在A杆上,现要将套在A柱上的盘换到C柱上,要求每次只能搬动一个,而且任何不允许将大盘套在小盘上面,假定有三柱子A,B,C可供使用。
个圆盘依其半径大小,大的在下,小的在上套在A杆上,现要将套在A柱上的盘换到C柱上,要求每次只能搬动一个,而且任何不允许将大盘套在小盘上面,假定有三柱子A,B,C可供使用。
现用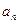 表示将n个圆盘全部从A柱上移到C上所至少需要移动的次数,回答下列问题:
表示将n个圆盘全部从A柱上移到C上所至少需要移动的次数,回答下列问题:
(1)写出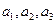 ,并求出
,并求出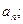
(2)记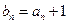 ,求和
,求和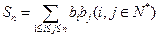 ;
;
(其中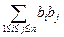 表示所有的积
表示所有的积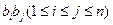 的和)
的和)
(3)证明: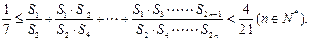
(本小题满分12分)
已知数列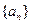 满足:
满足: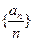 是公差为1的等差数列,且
是公差为1的等差数列,且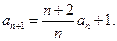
(1)求数列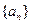 的通项公式
的通项公式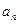 ;
;
(2)设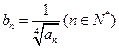 ,求证:
,求证: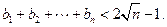
(本小题满分12分)
已知点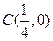 ,椭圆
,椭圆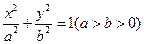 的右准线
的右准线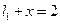 与x轴相交于点D,右焦点F到上顶点的距离为
与x轴相交于点D,右焦点F到上顶点的距离为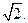
(1)求椭圆的方程;
(2)是否存在过点F且与x轴不垂直的直线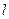 与椭圆交于A、B两点,使得
与椭圆交于A、B两点,使得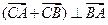 ?若存在,求出直线
?若存在,求出直线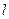 ;若不存在,说明理由。
;若不存在,说明理由。