在锐角 中,
中,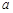 、
、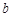 、
、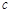 分别为角
分别为角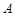 、
、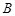 、
、 所对的边,且
所对的边,且 .
.
(1)求角 的大小;
的大小;
(2)若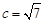 ,且
,且 的面积为
的面积为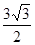 ,求
,求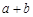 的值.
的值.
已知f(x)=x2-2(n+1)x+n2+5n-7,
(1)设f(x)的图象的顶点的纵坐标构成数列{an},求证:{an}为等差数列;
(2)设f(x)的图象的顶点到x轴的距离构成数列{bn},求{bn}的前n项和Sn.
已知等差数列{an}中,a3a7=-16,a4+a6=0,求{an}前n项和Sn.
已知{an}是正数组成的数列,a1=1,且点(,an+1)(n∈N+)在函数y=x2+1的图象上.
(1)求数列{an}的通项公式;
(2)若列数{bn}满足b1=1,bn+1=bn+2an,
求证:bn·bn+2<b.
如果数列的前n项和为Sn=an-3,求这个数列的通项公式.
在△ABC中,cos B=-,cos C=.
(1)求sin A的值;
(2)设△ABC的面积S△ABC=,求BC的长