在△ABC中,a,b,c分别是角A,B,C的对边,向量m=(2sinB,2-cos2B),n=(2sin2(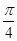 +
+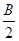 ),-1),且m⊥n.
),-1),且m⊥n.
(1)求角B的大小;
(2)求sinA+cosC的取值范围.
|
已知向量 ,求
,求
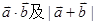 ;
;
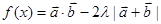 的最小值是
的最小值是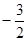 ,求实数
,求实数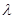 的值.
的值.
△ABC中,内角A,B,C的对边分别为a,b,c,已知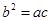 ,
, .
.
(1)求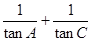 的值;
的值;
(2)设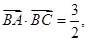 求
求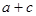 的值。
的值。
数列{an}是首项为23,公差为整数的等差数列,且第六项为正,第七项为负.
(1)求数列的公差.
(2)求前n项和Sn的最大值.
(3)当Sn>0时,求n的最大值.
已知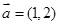 ,
,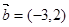 ,当
,当 为何值时,
为何值时,
(1)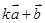 与
与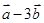 垂直?
垂直?
(2)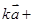
 与
与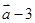
 平行?平行时它们是同向还是反向?
平行?平行时它们是同向还是反向?
已知函数 在同一半周期内的图象过点
在同一半周期内的图象过点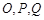 ,其中
,其中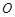 为坐标原点,
为坐标原点,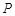 为函数
为函数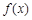 图象的最高点,
图象的最高点, 为函数
为函数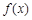 的图象与
的图象与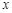 轴的正半轴的交点.
轴的正半轴的交点. 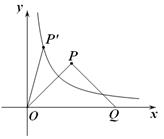
(1)求证: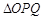 为等腰直角三角形.
为等腰直角三角形.
(2)将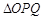 绕原点
绕原点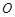 按逆时针方向旋转角
按逆时针方向旋转角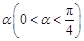 ,得到
,得到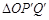 ,若点
,若点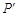 恰好落在曲线
恰好落在曲线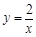
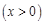 上(如图所示),试判断点
上(如图所示),试判断点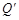 是否也落在曲线
是否也落在曲线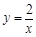
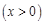 上,并说明理由
上,并说明理由