有一种密英文的明文(真实文)按字母分解，其中英文的a，b，c， ，z的26个字母(不分大小写)，依次对应1，2，3， ，26这26个自然数，见如下表格:
| a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
m |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
| n |
o |
p |
q |
r |
s |
t |
u |
v |
w |
x |
y |
z |
| 14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
给出如下变换公式: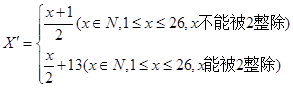
将明文转换成密文，如
，即
变成
；如
，即
变成
.
（1）按上述规定，将明文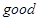
译成的密文是什么？
（2）按上述规定，若将某明文译成的密文是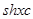
，那么原来的明文是什么？
（本小题满分12分）
小白鼠被注射某种药物后，只会表现为以下三种症状中的一种：兴奋、无变化（药物没有发生作用）、迟钝．若出现三种症状的概率依次为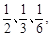
现对三只小白鼠注射这种药物．
（Ⅰ）求这三只小白鼠表现症状互不相同的概率；
（Ⅱ）用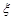
表示三只小白鼠共表现症状的种数，求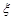的分布列及数学期望．
本小题满分12分）
已知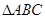
的三内角A，B，C所对三边分别为a，b，c，且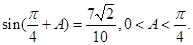
（I）求
的值；（II）若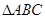的面积
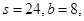求a的值．
已知数列
中，
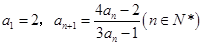，设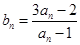
．
（Ⅰ）试写出数列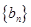
的前三项；
（Ⅱ）求证：数列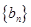是等比数列，并求数列的通项公式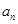
；
（Ⅲ）设的前
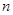项和为
，
求证：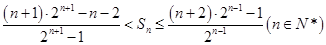
．
已知椭圆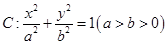
的左、右焦点分别为
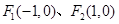，且经过定点
，
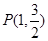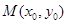为椭圆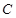
上的动点，以点
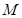为圆心，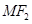
为半径作圆.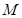
（1）求椭圆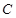的方程；
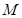（2）若圆与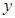
轴有两个不同交点，求点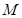横坐标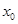
的取值范围；
（3）是否存在定圆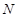
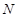，使得圆与圆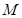恒相切？若存在，求出定圆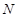的方程；若不存在，请说明理由.
某化工厂引进一条先进生产线生产某种化工产品，其生产的总成本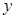
（万元）与年产量
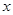（吨）之间的函数关系式可以近似地表示为
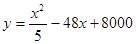，已知此生产线年产量最大为210吨。
（1）求年产量为多少吨时，生产每吨产品的平均成本最低，并求每吨产品平均最低成本；
（2）若每吨产品平均出厂价为40万元，那么当年产量为多少吨时，可以获得最大利润？最大利润是多少？