已知各项为实数的数列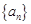 是等比数列, 且
是等比数列, 且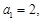
 数列
数列 满足:对任意正整数
满足:对任意正整数 ,有
,有 .
.
(1)求数列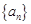 与数列
与数列 的通项公式;
的通项公式;
(2)在数列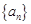 的任意相邻两项
的任意相邻两项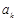 与
与 之间插入
之间插入 个
个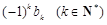 后,得到一个新的数列
后,得到一个新的数列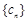 . 求数列
. 求数列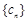 的前2012项之和.
的前2012项之和.
东海水晶制品厂去年的年产量为10万件,每件水晶产品的销售价格为100元,固定成本为80元.从今年起,工厂投入100万元科技成本,并计划以后每年比上一年多投入100万元科技成本.预计产量每年递增1万件,每件水晶产品的固定成本g(n)与科技成本的投入次数n的关系是g(n)= .若水晶产品的销售价格不变,第n次投入后的年利润为f(n)万元.
.若水晶产品的销售价格不变,第n次投入后的年利润为f(n)万元.
(1)求出f(n)的表达式.
(2)求从今年算起第几年利润最高?最高利润为多少万元?
某公司计划2014年在A,B两个电视台做总时间不超过300分钟的广告,广告总费用不超过9万元.A,B两个电视台的广告收费标准分别为500元/分钟和200元/分钟,假定A,B两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为0.3万元和0.2万元.问该公司如何分配在两个电视台做广告的时间,才能使公司的收益最大?最大收益是多少万元?
已知函数y= 的定义域为R.
的定义域为R.
(1)求a的取值范围.
(2)若函数的最小值为 ,解关于x的不等式x2-x-a2-a<0.
,解关于x的不等式x2-x-a2-a<0.
某公司租赁甲、乙两种设备生产A,B两类产品,甲种设备每天能生产A类产品5件和B类产品10件,乙种设备每天能生产A类产品6件和B类产品20件.已知设备甲每天的租赁费为200元,设备乙每天的租赁费为300元,现该公司要生产A类产品至少50件,B类产品至少140件,所需租赁费最多不超过2500元,写出满足上述所有不等关系的不等式.
已知x,y为正实数,满足1≤lg(xy)≤2,3≤lg ≤4,求lg(x4y2)的取值范围.
≤4,求lg(x4y2)的取值范围.