设函数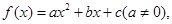 曲线y=f(x)通过点(0,2a+3),且在点
曲线y=f(x)通过点(0,2a+3),且在点
(-1,f(-1))处的切线垂直于y轴.
(1)用a分别表示b和c;
(2)当bc取得最小值时,求函数g(x)= 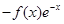 的单调区间.
的单调区间.
已知抛物线
 ,准线与
,准线与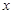 轴的交点为
轴的交点为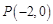 .
.
(Ⅰ)求抛物线 的方程;
的方程;
(Ⅱ)如图,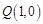 ,过点
,过点 的直线
的直线 与抛物线
与抛物线 交于不同的两点
交于不同的两点 ,AQ与BQ分别与抛物线
,AQ与BQ分别与抛物线 交于点
交于点
C,D,设AB,DC的斜率分别为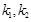 ,
,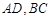 的斜率分别为
的斜率分别为 ,问:是否存在常数
,问:是否存在常数 ,使得
,使得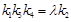 ,
,
若存在,求出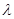 的值,若不存在,说明理由.
的值,若不存在,说明理由.
已知各项均为正数的数列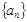 的前
的前 项和为
项和为 ,且
,且 . 在数列
. 在数列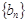 中,
中,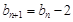 ,
, .
.
(Ⅰ)求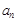 ,
,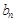 ;
;
(Ⅱ)设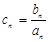 求数列
求数列 的前项和
的前项和 .
.
如图所示,四棱锥P-ABCD中,底面ABCD为菱形,且直线PA⊥平面ABCD,又棱PA=AB=2,E为CD的中点, .
.
(Ⅰ)求证:直线EA⊥平面PAB;
(Ⅱ)求直线AE与平面PCD所成角的正切值.
在△ABC中,角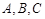 所对的边分别是
所对的边分别是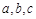 ,且满足:
,且满足: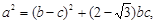 又
又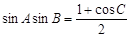 .
.
(Ⅰ)求角A的大小;
(Ⅱ)若a=2,求△ABC的面积S.
在单调递增数列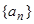 中,
中,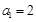 ,
,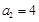 ,且
,且 成等差数列,
成等差数列,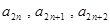 成等比数列,
成等比数列,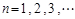 .
.
(Ⅰ)(ⅰ)求证:数列 为等差数列;
为等差数列;
(ⅱ)求数列 的通项公式.
的通项公式.
(Ⅱ)设数列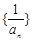 的前
的前 项和为
项和为 ,证明:
,证明: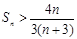 ,
,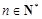 .
.