已知各项均不相等的等差数列{an}的前n项和为Sn,若S3=15,且a3+1为a1+1和a7+1的等比中项.
(1)求数列{an}的通项公式与前n项和Sn;
(2)设Tn为数列{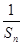 }的前n项和,问是否存在常数m,使Tn=m[
}的前n项和,问是否存在常数m,使Tn=m[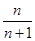 +
+ ],若存在,求m的值;若不存在,说明理由.
],若存在,求m的值;若不存在,说明理由.
为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法,某媒体在该地区选择了3600人调查,就是否“取消英语听力”的问题,调查统计的结果如下表:
|
应该取消 |
应该保留 |
无所谓 |
||
| 在校学生 |
2100人 |
120人 |
y人 |
||
| 社会人士 |
600人 |
x人 |
z人 |
已知在全体样本中随机抽取1人,抽到持“应该保留”态度的人的概率为0.05.
(1)现用分层抽样的方法在所有参与调查的人中抽取360人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(2)在持“应该保留”态度的人中,用分层抽样的方法抽取6人平均分成两组进行深入交流,求第一组中在校学生人数ξ的分布列和数学期望.
经销商经销某种农产品,在一个销售季度内,每售出1t该产品获利润500元,未售出的产品,每1t亏损300元。根据历史资料,得到销售季度内市场需求量的频率分布直方图,如右图所示。经销商为下一个销售季度购进了130t该农产品。以x(单位:t,100≤x≤150)表示下一个销售季度内经销该农产品的数量,T表示利润.
(1)将T表示为x的函数
(2)根据直方图估计利润T不少于57000元的概率;
(3)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值需求量落入该区间的频率作为需求量取该区间中点值的概率(例如:若x ,则取x=105,且x=105的概率等于需求量落入[100,110
,则取x=105,且x=105的概率等于需求量落入[100,110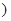 ,求T的数学期望.
,求T的数学期望.
设袋子中装有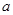 个红球,
个红球,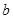 个黄球,
个黄球,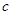 个蓝球,且规定:取出一个红球得1分,
个蓝球,且规定:取出一个红球得1分,
取出一个黄球2分,取出蓝球得3分。
(1)当 时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量
时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量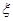 为取出此2球所得分数之和,.求
为取出此2球所得分数之和,.求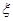 分布列;
分布列;
(2)从该袋子中任取(且每球取到的机会均等)1个球,记随机变量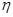 为取出此球所得分数.若
为取出此球所得分数.若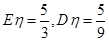 ,求
,求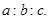
一个盒子里装有7张卡片, 其中有红色卡片4张, 编号分别为1, 2, 3, 4; 白色卡片3张, 编号分别为2, 3, 4.从盒子中任取4张卡片 (假设取到任何一张卡片的可能性相同).
(1)求取出的4张卡片中, 含有编号为3的卡片的概率.
(2)再取出的4张卡片中, 红色卡片编号的最大值设为X, 求随机变量X的分布列和数学期望.
在一场娱乐晚会上, 有5位民间歌手(1至5号)登台演唱, 由现场数百名观众投票选出最受欢迎歌手.各位观众须彼此独立地在选票上选3名选手, 其中观众甲是1号歌手的歌迷, 他必选1号, 不选2号, 另在3至5号中随机选2名.观众乙和丙对5位歌手的演唱没有偏爱, 因此在1至5号中随机选3名歌手.
(1)求观众甲选中3号歌手且观众乙未选中3号歌手的概率;
(2)X表示3号歌手得到观众甲、乙、丙的票数之和, 求X的分布列和数学期望.