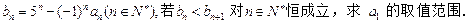已知数列{an}中,a1=2,an-an-1-2n=0(n≥2,n∈N*).
(1)写出a2,a3的值(只写结果),并求出数列{an}的通项公式;
(2)设bn=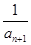 +
+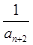 +
+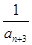 +…+
+…+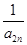 ,若对任意的正整数n,当m∈[-1,1]时,不等式t2-2mt+
,若对任意的正整数n,当m∈[-1,1]时,不等式t2-2mt+ >bn恒成立,求实数t的取值范围.
>bn恒成立,求实数t的取值范围.
C. 选修4-4:坐标系与参数方程.
已知在直角坐标系x0y内,直线l的参数方程为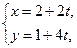 (t为参数).以Ox为极轴建立极坐标系,圆C的极坐标方程为
(t为参数).以Ox为极轴建立极坐标系,圆C的极坐标方程为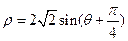 .
.
(1)写出直线l的普通方程和圆C的直角坐标方程;
(2)判断直线l和圆C的位置关系.
B. 选修4-2:矩阵与变换
已知 , 求矩阵B.
, 求矩阵B.
A. 选修4-1:几何证明选讲
已知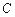 点在圆
点在圆 直径
直径 的延长线上,
的延长线上, 切圆
切圆 于
于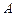 点,
点, 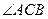 的平分线分别交
的平分线分别交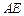 、
、 于点
于点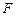 、
、 .
.
(1)求 的度数;
的度数;
(2)若 ,求
,求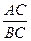 的值.
的值.
已知函数 .
.
(Ⅰ)当 时,求函数
时,求函数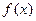 的最小值;
的最小值;
(Ⅱ)若函数 的图像在点
的图像在点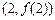 处的切线的倾斜角为
处的切线的倾斜角为 ,对于任意
,对于任意 ,函数
,函数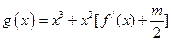 在区间
在区间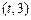 上总不是单调函数,求
上总不是单调函数,求 的取值范围;
的取值范围;
(Ⅲ)求证:  .
.
已知数列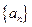 的前n项和为
的前n项和为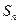 ,数列
,数列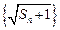 是公比为2的等比数列.
是公比为2的等比数列.
(Ⅰ)若 ,求
,求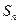 ;
;
(Ⅱ)探究数列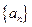 成等比数列的充要条件,并证明你的结论;
成等比数列的充要条件,并证明你的结论;
(Ⅲ)设