李明在10场篮球比赛中的投篮情况统计如下(假设各场比赛相互独立):
| 场次 |
投篮次数 |
命中次数 |
场次 |
投篮次数 |
命中次数 |
| 主场1 |
22 |
12 |
客场1 |
18 |
8 |
| 主场2 |
15 |
12 |
客场2 |
13 |
12 |
| 主场3 |
12 |
8 |
客场3 |
21 |
7 |
| 主场4 |
23 |
8 |
客场4 |
18 |
15 |
| 主场5 |
24 |
20 |
客场5 |
25 |
12 |
(1)从上述比赛中随机选择一场,求李明在该场比赛中投篮命中率超过0.6的概率;
(2)从上述比赛中随机选择一个主场和一个客场,求李明的投篮命中率一场超过0.6,一场不超过0.6的概率;
(3)记 为表中10个命中次数的平均数,从上述比赛中随机选择一场,记
为表中10个命中次数的平均数,从上述比赛中随机选择一场,记 为李明在这场比赛中的命中次数,比较
为李明在这场比赛中的命中次数,比较 与
与 的大小(只需写出结论)
的大小(只需写出结论)
(本小题满分10分)如图,在四棱锥S—ABCD中,侧棱SA=SB=SC=SD,底面ABCD是菱形,AC与BD交于O点.
(Ⅰ)求证:AC⊥平面SBD;
(Ⅱ)若E为BC中点,点P在侧面△SCD内及其边界上运动,并保持PE⊥AC,试指出动点P的轨迹,并证明你的结论.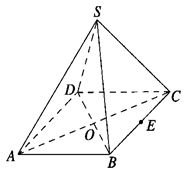
(本小题满分12分)如图,直三棱柱ABC—A1B1C1中,已知AC =BC = AA1=a,
∠ACB =90°,D 是A1B1中点.
(Ⅰ)求证:C1D ⊥平面A1B1BA ;
(Ⅱ)请问, 当点F 在BB1上什么位置时,会使得AB1⊥平面C1DF ?并证明你的结论.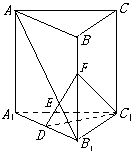
(本小题满分9分)已知圆C: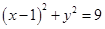 内有一点P(2,2),过点P作直线l交圆C于A、B两点.
内有一点P(2,2),过点P作直线l交圆C于A、B两点.
(Ⅰ)当l经过圆心C时,求直线l的方程;
(Ⅱ)当弦AB被点P平分时,写出直线l的方程;
(Ⅲ)当直线l的倾斜角为45º时,求弦AB的长.
(本小题满分9分)如图,圆锥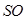 中,
中,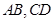 为底面圆的两条直径,
为底面圆的两条直径,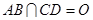 ,且
,且 ⊥
⊥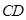 ,
,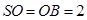 ,
, 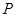 为
为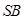 的中点.
的中点.
(Ⅰ)求证: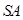 ∥平面
∥平面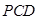 ;
;
(Ⅱ)求圆锥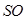 的表面积;
的表面积;
(Ⅲ)求异面直线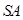 与
与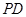 所成角的正切值.
所成角的正切值.
(本小题满分12分)分别求满足下列条件的直线方程.
(Ⅰ)过点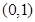 ,且平行于
,且平行于 :
: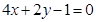 的直线;
的直线;
(Ⅱ)与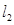 :
: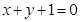 垂直,且与点
垂直,且与点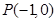 距离为
距离为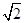 的直线.
的直线.