将圆上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线.
(1)写出的参数方程;
(2)设直线与的交点为,以坐标原点为极点,轴正半轴为极坐标建立极坐标系,求过线段的中点且与垂直的直线的极坐标方程.
如图,已知椭圆 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,以该椭圆上的点和椭圆的左、右焦点F1、F2为顶点的三角形的周长为4(
,以该椭圆上的点和椭圆的左、右焦点F1、F2为顶点的三角形的周长为4( +1),一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D.
+1),一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D. 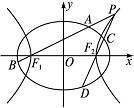
(1)求椭圆和双曲线的标准方程;
(2)设直线PF1、PF2的斜率分别为k1、k2,证明:k1·k2=1;
(3)是否存在常数λ,使得|AB|+|CD|=λ|AB|·|CD|恒成立?若存在,求λ的值;若不存在,请说明理由.
设函数 ,
, ,
, ,且以
,且以 为最小正周期.
为最小正周期.
(1)求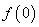 ;
;
(2)求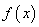 的解析式;
的解析式;
(3)已知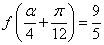 ,求
,求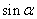 的值.
的值.
已知圆C与两坐标轴都相切,圆心C到直线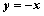 的距离等于
的距离等于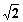 .
.
(1)求圆C的方程.
(2)若直线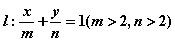 与圆C相切,求
与圆C相切,求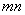 的最小值.
的最小值.
在锐角△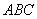 中,
中,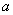 、
、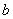 、
、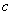 分别为角
分别为角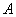 、
、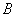 、
、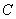 所对的边,且
所对的边,且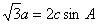
(1)确定角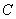 的大小;
的大小;
(2)若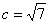 ,且△
,且△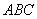 的面积为
的面积为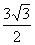 ,求
,求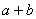 的值.
的值.
已知双曲线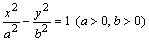 的右顶点为A,右焦点为F,右准线与
的右顶点为A,右焦点为F,右准线与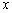 轴交于点B,且与一条渐近线交于点C,点O为坐标原点,
轴交于点B,且与一条渐近线交于点C,点O为坐标原点,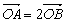 ,
, ,过点F的直线
,过点F的直线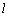 与双曲线右支交于点
与双曲线右支交于点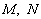 .
.
(Ⅰ)求此双曲线的方程;
(Ⅱ)求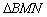 面积的最小值.
面积的最小值.