已知常数 ,向量
,向量 ,经过定点
,经过定点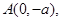 以
以 为方向向量的直线与经过定点
为方向向量的直线与经过定点 以
以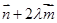 为方向向量的直线相交于
为方向向量的直线相交于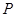 ,其中
,其中 ,
,
(1)求点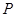 的轨迹
的轨迹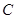 的方程;(2)若
的方程;(2)若 ,过
,过 的直线交曲线
的直线交曲线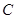 于
于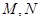 两点,求
两点,求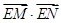 的取值范围。
的取值范围。
以椭圆 的一个顶点
的一个顶点 为直角顶点作此椭圆的内接等腰直角三角形
为直角顶点作此椭圆的内接等腰直角三角形 ,试问:(1)这样的等腰直角三角形是否存在?若存在,写出一个等腰直角三角形两腰所在的直线方程。若不存在,说明理由。(2)这样的等腰直角三角形若存在,最多有几个?
,试问:(1)这样的等腰直角三角形是否存在?若存在,写出一个等腰直角三角形两腰所在的直线方程。若不存在,说明理由。(2)这样的等腰直角三角形若存在,最多有几个?
在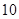 个同样型号的产品中,有
个同样型号的产品中,有 个是正品,
个是正品,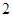 个是次品,从中任取
个是次品,从中任取 个,求(1)其中所含次品数
个,求(1)其中所含次品数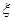 的期望、方差;(2)事件“含有次品”的概率。
的期望、方差;(2)事件“含有次品”的概率。
已知椭圆 ,直线
,直线 是直线上的线段,且
是直线上的线段,且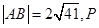 是椭圆上一点,求
是椭圆上一点,求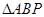 面积的最小值。
面积的最小值。
一动圆截直线 和直线
和直线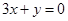 所得弦长分别为
所得弦长分别为 ,求动圆圆心的轨迹方程。
,求动圆圆心的轨迹方程。