随机将这个连续正整数分成两组,每组个数,组最小数为,最大数为;组最小数为,最大数为,记
(1)当时,求的分布列和数学期望;
(2)令表示事件与的取值恰好相等,求事件发生的概率;
(3)对(2)中的事件,表示的对立事件,判断和的大小关系,并说明理由。
某厂生产某种零件,每个零件的成本为 元,出厂单价定为
元,出厂单价定为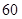 元.该厂为鼓励销售商订购,决定当一次订购量超过
元.该厂为鼓励销售商订购,决定当一次订购量超过 个时,凡多订购一个,订购的全部零件的出厂单价就降低
个时,凡多订购一个,订购的全部零件的出厂单价就降低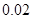 元,但实际出厂单价不能低于
元,但实际出厂单价不能低于 元.
元.
(Ⅰ)当一次订购量为多少时,零件的实际出厂单价恰降为 元?
元?
(Ⅱ)设一次订购量为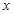 个,零件的实际出厂单价为
个,零件的实际出厂单价为 元,写出函数
元,写出函数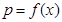 的表达式;
的表达式;
(Ⅲ)当销售商一次订购 个零件时,该厂获得的利润是多少元?如果订购
个零件时,该厂获得的利润是多少元?如果订购 个,利润又是多少元?
个,利润又是多少元?
已知函数 在定义域
在定义域 上单调递减,又当
上单调递减,又当 ,且
,且 时,
时, .
.
(Ⅰ)证明 是奇函数; (Ⅱ)求不等式
是奇函数; (Ⅱ)求不等式 的解集.
的解集.
(本小题满分14分)已知函数 是一次函数且在
是一次函数且在 上为增函数,若
上为增函数,若 .
.
(Ⅰ)求 的解析式;(Ⅱ)试比较
的解析式;(Ⅱ)试比较 与
与 的大小.
的大小.
已知

 ,复数
,复数 ,当
,当 为何值时,
为何值时,
(Ⅰ) ;(Ⅱ)
;(Ⅱ) 是纯虚数;(Ⅲ)
是纯虚数;(Ⅲ)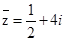 .
.
(本题满分14分)已知集合
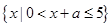 ,集合
,集合

(Ⅰ)若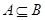 ,求实数
,求实数 的取值范围;
的取值范围;
(Ⅱ)若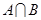 是单元素集合求实数
是单元素集合求实数 的值.
的值.