在平面直角坐标系中,椭圆的离心率为,直线被椭圆截得的线段长为.
(Ⅰ)求椭圆的方程;
(Ⅱ)过原点的直线与椭圆交于两点(不是椭圆的顶点).点在椭圆上,且,直线与轴、轴分别交于两点.
(i)设直线的斜率分别为,证明存在常数使得,并求出的值;
(ii)求面积的最大值.
已知函数
(1)若 ,求
,求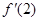 的值;
的值;
(2)若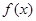 的图像与直线
的图像与直线 相切于点
相切于点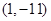 ,求
,求 的值;
的值;
(3)在(2)的条件下,求函数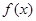 的单调区间.
的单调区间.
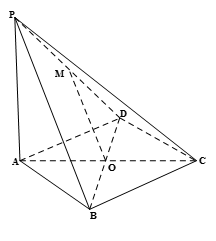
如图 ,在四棱锥
,在四棱锥 中,
中,
 平面
平面 ,底面
,底面 是菱形,点O是对角线
是菱形,点O是对角线 与
与 的交点,
的交点, 是
是 的中点,
的中点, .
.
(1) 求证: 平面
平面 ;
;
(2) 平面
 平面
平面 ;
;
(3) 当四棱锥 的体积等于
的体积等于 时,求
时,求 的长.
的长.
某校为了解学生的学科学习兴趣,对初高中学生做了一个喜欢数学和喜欢语文的抽样调查,随机抽取了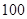 名学生,相关的数据如下表所示:
名学生,相关的数据如下表所示:
| 数学 |
语文 |
总计 |
|
| 初中 |
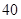 |
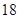 |
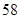 |
| 高中 |
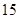 |
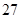 |
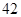 |
| 总计 |
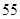 |
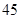 |
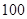 |
(1) 用分层抽样的方法从喜欢语文的学生中随机抽取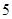 名,高中学生应该抽取几名?
名,高中学生应该抽取几名?
(2) 在(1)中抽取的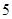 名学生中任取
名学生中任取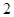 名,求恰有
名,求恰有 名初中学生的概率.
名初中学生的概率.
设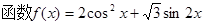
(1)求函数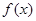 的最小正周期和单调递增区间
的最小正周期和单调递增区间
(2)当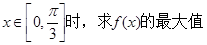
已知函数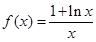

(1)求函数f(x)的极值;
(2)如果当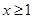 时,不等式
时,不等式 恒成立,求实数k的取值范围;
恒成立,求实数k的取值范围;
(3)求证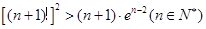 .
.