设函数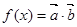 ,其中向量
,其中向量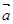 =(2cosx,1),
=(2cosx,1),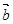 =(cosx,
=(cosx, sin2x),x∈R.
sin2x),x∈R.
(1)若f(x)=1- 且x∈[-
且x∈[-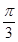 ,
,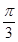 ],求x;
],求x;
(2)若函数y=2sin2x的图象按向量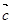 =(m,n)(|m|<
=(m,n)(|m|<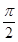 )平移后得到函数y=f(x)的图象,求实数m、n的值.
)平移后得到函数y=f(x)的图象,求实数m、n的值.
解关于x的不等式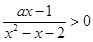
在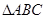 中,角
中,角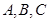 所对的边分别为
所对的边分别为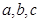 ,且满足
,且满足 ,
,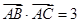 .
.
(1) 求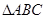 的面积;
的面积;
(2)若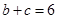 ,求
,求 的值.
的值.
(本小题满分13分)已知数列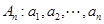 .如果数列
.如果数列 满足
满足 ,
,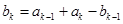 ,其中
,其中 ,则称
,则称 为
为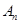 的“衍生数列”.
的“衍生数列”.
(Ⅰ)写出数列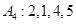 的“衍生数列”
的“衍生数列” ;
;
(Ⅱ)若 为偶数,且
为偶数,且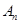 的“衍生数列”是
的“衍生数列”是 ,证明:
,证明: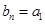 ;
;
(Ⅲ)若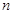 为奇数,且
为奇数,且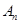 的“衍生数列”是
的“衍生数列”是 ,
, 的“衍生数列”是
的“衍生数列”是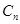 ,….依次将数
,….依次将数
列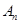 ,
, ,
,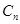 ,…的首项取出,构成数列
,…的首项取出,构成数列 .证明:
.证明: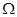 是等差数列.
是等差数列.
(本小题满分14分)已知椭圆
 的一个焦点是
的一个焦点是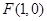 ,且离心率为
,且离心率为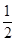 .
.
(Ⅰ)求椭圆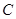 的方程;
的方程;
(Ⅱ)设经过点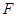 的直线交椭圆
的直线交椭圆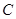 于
于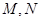 两点,线段
两点,线段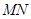 的垂直平分线交
的垂直平分线交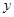 轴于点
轴于点 ,求
,求 的取值范围.
的取值范围.