已知: (
( )是方程
)是方程 的两根,且
的两根,且 ,
, .
.  (1)求
(1)求 的值;(2)设
的值;(2)设 ,求证:
,求证: ;(3)求证:对
;(3)求证:对 有
有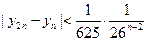 w。.w..
w。.w..
设函数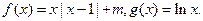 (1)当
(1)当 时,求函数
时,求函数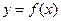 在
在 上的最大值;(2)记函数
上的最大值;(2)记函数 ,若函数
,若函数 有零点,求
有零点,求 的取值范围.
的取值范围.
已知如图,椭圆方程为
 .P为椭圆上的动点,
.P为椭圆上的动点,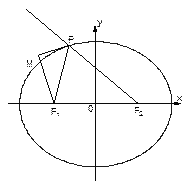
F1、F2为椭圆的两焦点,当点P不在x轴上时,过F1作∠F1PF2的外角
平分线的垂线F1M,垂足为M,当点P在x轴上时,定义M与P重合.
(1)求M点的轨迹T的方程;(2)已知 、
、 ,
,
试探究是否存在这样的点 :
: 是轨迹T内部的整点
是轨迹T内部的整点
(平面内横、纵坐标均为整数的点称为整点),且△OEQ的面积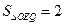 ?
?
若存在,求出点Q的坐标,若不存在,说明理由.
右图为一简单组合体,其底面ABCD为正方形, 平面
平面 ,
,
 ,且
,且 ,(1)求证:BE//平面PDA;
,(1)求证:BE//平面PDA;
(2)若N为线段 的中点,求证:
的中点,求证: 平面
平面 ;
;
(3)若 ,求平面PBE与平面ABCD所成的二面角的大小.
,求平面PBE与平面ABCD所成的二面角的大小.
已知复数 ,
, ,且
,且 .(1)若
.(1)若 且
且
 ,求
,求 的值;(2)设
的值;(2)设 =
= ,已知当
,已知当 时,
时,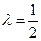 ,试求
,试求 的值.
的值.