为了降低能源损耗,某体育馆的外墙需要建造隔热层.体育馆要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度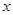 (单位:cm)满足关系:
(单位:cm)满足关系: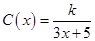 (
(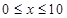 ,
,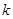 为常数),若不建隔热层,每年能源消耗费用为8万元.设
为常数),若不建隔热层,每年能源消耗费用为8万元.设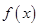 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.
(1)求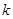 的值及
的值及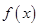 的表达式;
的表达式;
(2)隔热层修建多厚时,总费用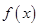 达到最小?并求出最小值.
达到最小?并求出最小值.
设f(x)=x2+px+q,A={x|x=f(x)},B={x|f[f(x)]=x}.
(1)求证:A B;
B;
(2)如果A={-1,3},求B。
已知集合A={z||z-2|≤2,z∈C},集合B={w|w=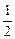 zi+b,b∈R},当A∩B=B时,求b的值.
zi+b,b∈R},当A∩B=B时,求b的值. 
已知{an}是等差数列,d为公差且不为0,a1和d均为实数,它的前n项和记作Sn,设集合A={(an,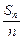 )|n∈N*},B={(x,y)|
)|n∈N*},B={(x,y)| x2-y2=1,x,y∈R}.
x2-y2=1,x,y∈R}.
试问下列结论是否正确,如果正确,请给予证明;如果不正确,请举例说明
(1)若以集合A中的元素作为点的坐标,则这些点都在同一条直线上;
(2)A∩B至多有一个元素;
(3)当a1≠0时,一定有A∩B≠ .
.
已知集合A={(x,y)|x2+mx-y+2=0},B={(x,y)|x-y+1=0,且0≤x≤2},如果A∩B≠ ,求实数m的取值范围.
,求实数m的取值范围.
向50名学生调查对A、B两事件的态度,有如下结果: 赞成A的人数是全体的五分之三,其余的不赞成,赞成B的比赞成A的多3人,其余的不赞成;另外,对A、B都不赞成的学生数比对A、B都赞成的学生数的三分之一多1人. 问对A、B都赞成的学生和都不赞成的学生各有多少人?