已知{an}是等差数列,d为公差且不为0,a1和d均为实数,它的前n项和记作Sn,设集合A={(an,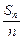 )|n∈N*},B={(x,y)|
)|n∈N*},B={(x,y)| x2-y2=1,x,y∈R}.
x2-y2=1,x,y∈R}.
试问下列结论是否正确,如果正确,请给予证明;如果不正确,请举例说明
(1)若以集合A中的元素作为点的坐标,则这些点都在同一条直线上;
(2)A∩B至多有一个元素;
(3)当a1≠0时,一定有A∩B≠ .
.
如图,已知矩形ABCD中,AB=10,BC=6,将矩形沿对角线BD把△ABD折起,使A移到A1点,且A1在平面BCD上的射影O恰好在CD上.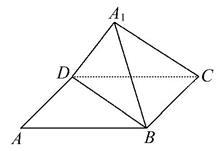
(1)求证:BC⊥A1D.
(2)求证:平面A1BC⊥平面A1BD.
(3)求三棱锥A1-BCD的体积.
已知点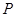 (0,5)及圆
(0,5)及圆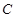 :
: .
.
(1)若直线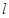 过
过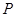 且被圆C截得的线段长为4
且被圆C截得的线段长为4 ,求
,求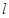 的方程;
的方程;
(2)求过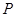 点的圆
点的圆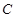 的弦的中点的轨迹方程.
的弦的中点的轨迹方程.
如图所示,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠ADC=45°,AD=AC=1,O为AC的中点,PO⊥平面ABCD,PO=2,M为PD的中点.
(1)证明:PB∥平面ACM;
(2)证明:AD⊥平面PAC.
(1)求与直线 垂直,且与原点的距离为6的直线方程;
垂直,且与原点的距离为6的直线方程;
(2)求经过直线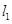 :
: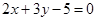 与
与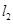 :
: 的交点,且平行于直线
的交点,且平行于直线 的直线方程.
的直线方程.
某校学生研究性学习小组发现,学生上课的注意力指标随着听课时间的变化而变化,老师讲课开始时,学生的兴趣激增;接下来学生的兴趣将保持较理想的状态一段时间,随后学生的注意力开始分散.设f(t)表示学生注意力指标,该小组发现f(t)随时间t(分钟)的变化规律(f(t)越大,表明学生的注意力越集中)如下: (a>0,且a≠1)
(a>0,且a≠1)
若上课后第5分钟时的注意力指标为140,回答下列问题:
(Ⅰ)求a的值;
(Ⅱ)上课后第5分钟时和下课前5分钟时比较,哪个时间注意力更集中?
(Ⅲ)在一节课中,学生的注意力指标至少达到140的时间能保持多长?