（1）求证：当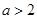
时，
；
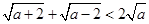（2）证明：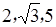
不可能是同一个等差数列中的三项.
已知曲线
上的动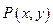点
满足到点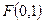
的距离比到直线
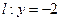的距离小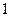
．
（1）求曲线的方程；
（2）动点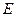
在直线
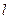上，过点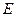分别作曲线的切线
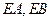，切点为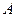
、
．
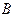（ⅰ）求证：直线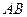
恒过一定点，并求出该定点的坐标；
（ⅱ）在直线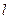上是否存在一点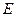，使得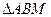
为等边三角形（
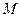点也在直线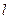上）？若存在,求出点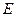坐标,若不存在,请说明理由
已知函数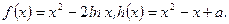
（1）求函数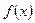
的极值；
（2）设函数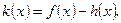
若函数
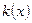在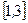
上恰有两个不同零点，求实数 
的取值范围.
如图，直角△BCD所在的平面垂直于正△ABC所在的平面，PA⊥平面ABC，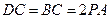
,
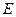、F分别为DB、CB的中点，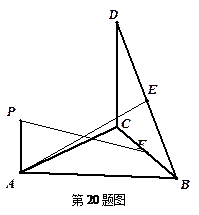
（1）证明：AE⊥BC；
（2）求直线PF与平面BCD所成的角.
已知数列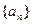
的前n项和为
（1）求
的值，并猜想出数列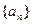的通项公式
（2）设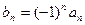
，请利用（I）的结论，求数列
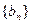的前15项和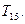
已知向量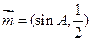
与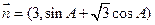
共线，其中A是△ABC的内角．
（1）求角
的大小；
（2）若BC=2，求△ABC面积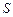
的最大值，并判断S取得最大值时△ABC的形状.