在2012~2013赛季NBA季后赛中,当一个球队进行完7场比赛被淘汰后,某个篮球爱好者对该队的7场比赛得分情况进行统计,如下表:
| 场次i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 得分xi |
100 |
104 |
98 |
105 |
97 |
96 |
100 |
为了对这个队的情况进行分析,此人设计计算σ的算法流程图如图所示(其中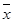 是这7场比赛的平均得分),求输出的σ的值.
是这7场比赛的平均得分),求输出的σ的值.
(本小题满分10分)

袋中有大小、形状相同的白、黑球各一个,现有放回地随机摸取3次,每次摸取一个球.
(Ⅰ)试问:一共有多少种不同的结果?请列出所有可能的结果;

(Ⅱ)若摸到白球时得1分,摸到黑球时得2分,求3次摸球所得总分大于4分的概率.
(本小题满分10分)
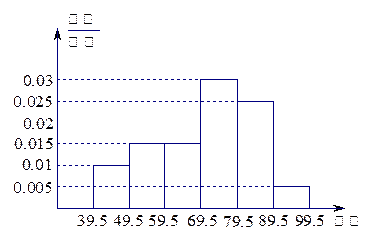
如下图,从参加数学竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如下. 观察图形,回答下列问题:
(Ⅰ)79.5—89.5这一组的频数、频率分别是多少?
(Ⅱ)估计这次数学竞赛的平均成绩是多少?
(Ⅲ)估计这次数学竞赛的及格率(60分及以上为及格).
|
(本小题满分8分)
在 中,
中,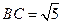 ,
,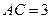 ,
,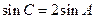 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求 的值.
的值.
(本小题满分8分)
在长方体 中,底面是边长为2的正方形,
中,底面是边长为2的正方形,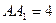 .
.
(Ⅰ)指出二面角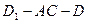 的平面角,并求出它的正切值;
的平面角,并求出它的正切值;
(Ⅱ)求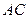 与
与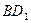 所成的角.
所成的角.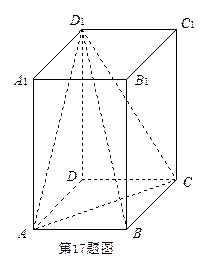
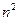 个正数排成如下表所示的
个正数排成如下表所示的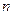 行
行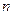 列:
列: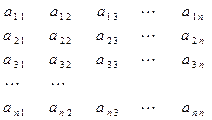
其中每一行成等差数列,每一列成等比数列,且各列的公比相等,若 ,
,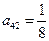 ,
,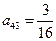 。
。
①求 ;
;
②记 ,求
,求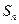 关于
关于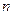 的表达式;
的表达式;
③对于②的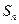 ,求证:
,求证: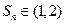 ;
;
④若集合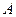 是集合
是集合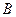 的真子集,则称由
的真子集,则称由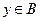 的判断到
的判断到 的判断为对
的判断为对 的估计的一次
的估计的一次
优化。请你优化③中的结果。