若不等式组 (其中
(其中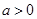 )表示的平面区域的面积是9.
)表示的平面区域的面积是9.
(1)求 的值;(2)求
的值;(2)求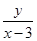 的最小值,及此时
的最小值,及此时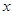 与
与 的值.
的值.
如图所示,长方体ABCD—A′B′C′D′中,用截面截下一个棱锥C—A′DD′,
求棱锥C—A′DD′的体积与剩余部分的体积之比.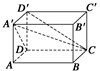
如图所示,半径为R的半圆内的阴影部分以直径AB所在直线为轴,旋转一周得到一几何体,求该几何体的表面积(其中∠BAC=30°)及其体积.
如图所示,长方体ABCD-A1B1C1D1中,AB=a,BC=b,BB1=c,并且a>b>c>0.
求沿着长方体的表面自A到C1的最短线路的长.
如图所示的几何体中,四边形AA1B1B是边长为3的正方形,CC1=2,CC1∥AA1,这个几何体是棱柱吗?若是,指出是几棱柱.若不是棱柱,请你试用一个平面截去一部分,使剩余部分是一个棱长为2的三棱柱,并指出截去的几何体的特征,在立体图中画出截面.
圆台的一个底面周长是另一个底面周长的3倍,轴截面的面积等于392 cm2,母线与轴的夹角是45°,求这个圆台的高、母线长和两底面半径.