函数
在
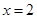时取得极小值.
（1）求实数
的值；
（2）是否存在区间
，使得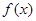
在该区间上的值域为
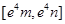？若存在，求出
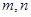的值；若不存在，请说明理由.
对于给定数列
，如果存在实常数
使得
对于任意
都成立，我们称数列是 “线性数列”．
（1）若
，
，，数列
、
是否为“线性数列”？若是，指出它对应的实常数
，若不是，请说明理由；
（2）证明：若数列是“线性数列”，则数列
也是“线性数列”；
（3）若数列满足
，
，
为常数．求数列前
项的和．
已知函数
，
.
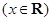（1）证明：函数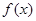
在区间
上为增函数，并指出函数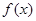在区间
上的单调性.
（2）若函数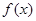的图像与直线
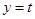有两个不同的交点
，
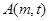，其中
，求
关于
的函数关系式.
（3）求的取值范围.
已知数列
为等差数列，公差
,且
（1）求证：当k取不同自然数时，此方程有公共根；
（2）若方程不同的根依次为
…,求证：数列
为等差数列.
已知
（1）求
的值；
（2）求
的值.
如图：三棱锥
中，
^底面
，若底面是边长为2的正三角形，且
与底面所成的角为
．若
是
的中点，求：
（1）三棱锥的体积；
（2）异面直线
与
所成角的大小（结果用反三角函数值表示）．