如图，货轮在海上B处，以50海里/时的速度沿方位角（从正北方向顺时针转到目标方向线的水平角）为155o的方向航行，为了确定船位，在B点处观测到灯塔A的方位角为125o．半小时后，货轮到达C点处，观测到灯塔A的方位角为80o．求此时货轮与灯塔之间的距离（答案保留最简根号）．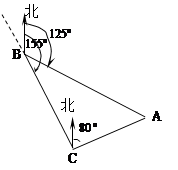 
（本小题满分12分）已知f (x)＝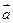
·
－1，其中向量＝（
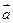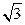sin2x，cosx），＝（1，2cosx）（x∈R）
（Ⅰ）求f (x)的单调递减区间；
（Ⅱ）在△ABC中，角A、B、C的对边分别为a、b、c，f (A)＝2，a＝
，b＝，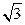
求边长c的值。
（本小题满分16分）过原点O作圆x2+y2-8x=0的弦OA。
求弦OA中点M的轨迹方程；
（2）如点
是（1）中的轨迹上的动点，
①求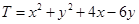
的最大、最小值；
②求
的最大、最小值。
（本小题满分14分）求圆心在直线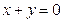
上，且过两圆
，
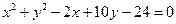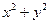
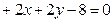交点的圆的方程。
（本小题满分14分）已知圆与y轴相切，圆心在直线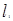
: x-3y=0上，且在直线
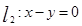上截得的弦长为
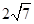，求该圆的方程.
（本小题满分14分）已知圆C：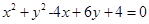
（1）将圆C的方程化成标准方程并指出圆心C的坐标及半径的大小；
（2）过点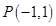
引圆C的切线，切点为A，求切线长
；
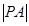（3）求过点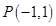的圆C的切线方程；