如图,在四棱锥P-ABCD中,底面ABCD是∠DAB=60°,且边长为a的菱形,侧面PAD为正三角形,其所在平面垂直底面ABCD.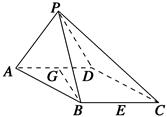
(1)若G为AD边的中点,求证:BG⊥平面PAD;
(2)求证:AD⊥PB;
(3)若E为BC边的中点,能否在棱PC上找到一点F,使平面DEF⊥平面ABCD,并证明你的结论.
(本题共12分)有一小型自来水厂,蓄水池中已有水450吨,水厂每小时可向蓄水池注水80吨,同时蓄水池向居民小区供水,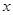 小时内供水总量为
小时内供水总量为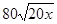 吨。现在开始向池中注水并同时向居民小区供水,问:
吨。现在开始向池中注水并同时向居民小区供水,问:
(1)多少小时后蓄水池中的水量最少?
(2)如果蓄水池中存水量少于150吨时,就会出现供水紧张,那么有几个小时供水紧张?
(本题共12分)设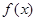 为定义在
为定义在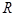 上的偶函数,当
上的偶函数,当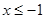 时,
时,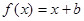 ,且
,且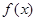 的图象经过点
的图象经过点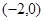 ,又在
,又在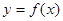 的图象中,有一部分是顶点为(0,2),且过
的图象中,有一部分是顶点为(0,2),且过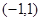 的一段抛物线。
的一段抛物线。
(1)试求出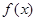 的表达式;
的表达式;
(2)求出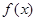 值域;
值域;
(本题共12分)
(1)计算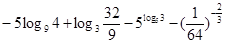
(2)解方程: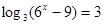
(本题共12分)设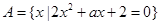 ,
,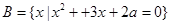 ,
, 。
。
(1)求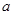 的值及
的值及 ;
;
(2)设全集 ,求 (∁I A)
,求 (∁I A) (∁I B);
(∁I B);
(3)写出(∁I A) (∁I B)的所有子集。
(∁I B)的所有子集。
如图,等腰梯形ABEF中,AB//EF,AB=2,AD=AF=1,AF⊥BF,O为AB的中点,矩形ABCD所在平面与平面ABEF互相垂直.
(1)求证:AF⊥平面CBF;
(2)在棱FC上是否存在点M,使得OM//平面DAF?
(3)求点A到平面BDF的距离.