甲、乙两个工厂,甲厂位于一直线河岸的岸边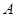 处,乙厂与甲厂在河的同侧,乙厂位于离河岸40千米的
处,乙厂与甲厂在河的同侧,乙厂位于离河岸40千米的 处,乙厂到河岸的垂足
处,乙厂到河岸的垂足 与
与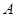 相距50千米,两厂要在此岸边
相距50千米,两厂要在此岸边 之间合建一个供水站
之间合建一个供水站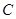 ,从供水站到甲厂和乙厂的水管费用分别为每千米3
,从供水站到甲厂和乙厂的水管费用分别为每千米3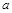 元和5
元和5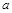 元,若
元,若 千米,设总的水管费用为
千米,设总的水管费用为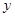 元,如图所示,
元,如图所示,
(1)写出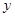 关于
关于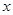 的函数表达式;
的函数表达式;
(2)问供水站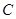 建在岸边何处才能使水管费用最省?
建在岸边何处才能使水管费用最省? 
请用程序框图表示前面讲过的“判断整数n(n>2)是否为质数”的算法.
这是中国古代的一个著名算法案例:鸡兔49头,100根腿往地里走,问鸡兔各多少?
由相应的程序框图如图,补充完整一个计算1+2+3+…+100的值的算法.(用循环结构) 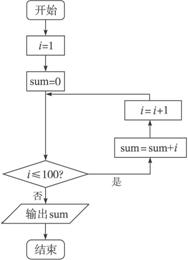
第一步,设i的值为_____________.
第二步,设sum的值为_____________.
第三步,如果i≤100执行第_____________步,否则,转去执行第_____________步.
第四步,计算sum+i并将结果代替_____________.
第五步,计算_____________并将结果代替i.
第六步,转去执行第三步.
第七步,输出sum的值并结束算法.
高中某班一共有40名学生,设计算法流程图,统计班级数学成绩良好(分数>80)和优秀(分数>90)的人数.
设计框图实现1+3+5+7+…+131的算法.