已知抛物线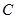 :
: 的焦点为圆
的焦点为圆 的圆心,直线
的圆心,直线 与
与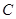 交于不同的两点
交于不同的两点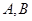 .
.
(1) 求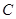 的方程;
的方程;
(2) 求弦长 。
。
如图,已知四棱锥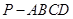 的底面是正方形,
的底面是正方形,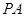 ⊥底面
⊥底面 ,且
,且 ,点
,点 、
、 分别为侧棱
分别为侧棱 、
、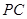 的中点
的中点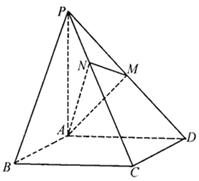
(1)求证: ∥平面
∥平面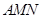 ;
;
(2)求证: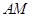 ⊥平面
⊥平面 .
.
(本小题满分12分)如图,椭圆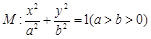 的离心率为
的离心率为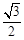 ,直线
,直线 和
和 所围成的矩形ABCD的面积为8.
所围成的矩形ABCD的面积为8.
(Ⅰ)求椭圆M的标准方程;
(Ⅱ) 设直线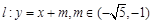 与椭圆M有两个不同的交点
与椭圆M有两个不同的交点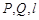 与矩形ABCD有两个不同的交点
与矩形ABCD有两个不同的交点 .求
.求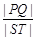 的最大值及取得最大值时m的值.
的最大值及取得最大值时m的值.
(本小题满分12分)设双曲线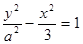 的两个焦点分别为
的两个焦点分别为 ,离心率为2.
,离心率为2.
(Ⅰ)求此双曲线的渐近线 的方程;
的方程;
(Ⅱ)若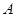 、
、 分别为
分别为 上的点,且
上的点,且 ,求线段
,求线段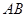 的中点
的中点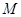 的轨迹方程,并说明轨迹是什么曲线;
的轨迹方程,并说明轨迹是什么曲线;
(本小题满分12分)抛物线 的焦点为F,
的焦点为F,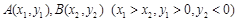 在抛物线上,且存在实数
在抛物线上,且存在实数 ,使
,使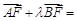
 ,
,
(Ⅰ)求直线AB的方程;
(Ⅱ)求△AOB的外接圆的方程。