(本小题满分12分)某厂生产某种零件,每个零件的成本为40元,出厂单价定为60元,该厂为鼓励销售商订购,决定当一次订购量超过100个时,每多订购一个,订购的全部零件的出厂单价就降低0.02元,但实际出厂单价不能低于51元.
(Ⅰ)当一次订购量为多少个时,零件的实际出厂单价恰降为51元?
(Ⅱ)设一次订购量为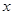 个,零件的实际出厂单价为
个,零件的实际出厂单价为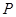 元,写出函数
元,写出函数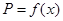 的表达式;
的表达式;
(Ⅲ)当销售商一次订购500个零件时,该厂获得的利润是多少元?如果订购1000个,利润又是多少元?(工厂售出一个零件的利润=实际出厂单价-成本)
(本小题满分12分)
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下表所示:
零件的个数 (个) (个) |
2 |
3 |
4 |
5 |
加工的时间 (小时) (小时) |
2.5 |
3 |
4 |
4.5 |
(Ⅰ)在给定的坐标系中画出表中数据的散点图;
(Ⅱ)求出 关于
关于 的线性回归方程
的线性回归方程 ,
,
并在坐标系中画出回归直线;
(Ⅲ)试预测加工10个零件需要多少时间?
(本小题满分12分)
已知 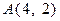 ,
,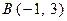 ,
,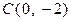 为坐标平面上的三个点,
为坐标平面上的三个点, 为坐标原点,点
为坐标原点,点 为
为 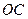 所在直线上一个动点.
所在直线上一个动点.
(Ⅰ)若 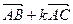 与
与  垂直,求
垂直,求  的值;
的值;
(Ⅱ)若向量  在向量
在向量 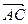 方向上的射影的数量为
方向上的射影的数量为  ,求
,求 点的坐标.
点的坐标.
(本小题满分12分)
已知函数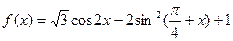 ,
,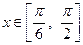 .
.
(Ⅰ)求 的最大值,并求出当
的最大值,并求出当 取得最大值时
取得最大值时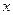 的取值;
的取值;
(Ⅱ)求  的单调递增区间.
的单调递增区间.
(本小题满分12分)
(Ⅰ)求 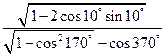 的值;
的值;
(Ⅱ)若 ,且
,且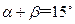 ,求
,求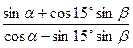 的值.
的值.
(本小题满分12分)在数列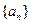 中,
中,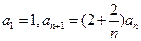
(1)设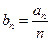 ,证明数列
,证明数列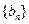 是等比数列并求数列
是等比数列并求数列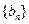 的通项公式
的通项公式
(2)求数列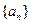 的前
的前 项和
项和