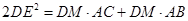(本小题满分12分)
已知 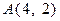 ,
,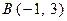 ,
,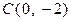 为坐标平面上的三个点,
为坐标平面上的三个点, 为坐标原点,点
为坐标原点,点 为
为 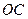 所在直线上一个动点.
所在直线上一个动点.
(Ⅰ)若 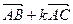 与
与  垂直,求
垂直,求  的值;
的值;
(Ⅱ)若向量  在向量
在向量 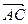 方向上的射影的数量为
方向上的射影的数量为  ,求
,求 点的坐标.
点的坐标.
(本小题满分12分)
某市统计局就某地居民的月收入调查了 10 000 人,并根据所得数据画出样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[1 000,1500)).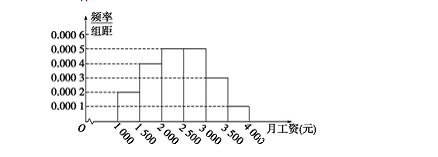
(1)求居民收入在[3 000,3 500)的频率;
(2)根据频率分布直方图算出样本数据的中位数;
(3)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这 10 000 人中按分层抽样方法抽出 100 人作进一步分析,则月收入在[2 500,3 000)的这段应抽取多少人?
(本小题满分12分)在锐角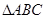 中,内角
中,内角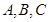 所对的边分别为
所对的边分别为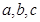 .已知
.已知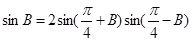
(1)求角 的大小;
的大小;
(2)若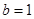 ,求
,求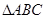 的面积的最大值
的面积的最大值
(本小题满分10分)选修4-5:不等式选讲
已知定义在R上的函数f(x)=|x+1|+|x-2|的最小值为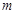 .
.
(Ⅰ)求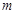 的值;
的值;
(Ⅱ)若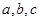 是正实数,且满足
是正实数,且满足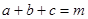 ,求证:
,求证: .
.
(本小题满分10分)选修4-4:坐标系与参数方程
将圆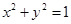 每一点的,横坐标保持不变,纵坐标变为原来的2倍,得到曲线C.
每一点的,横坐标保持不变,纵坐标变为原来的2倍,得到曲线C.
(Ⅰ)写出C的参数方程;
(Ⅱ)设直线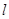 :
: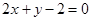 与C的交点为
与C的交点为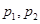 ,以坐标原点为极点,
,以坐标原点为极点,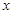 轴的正半轴为极轴建立极坐标系,求线段
轴的正半轴为极轴建立极坐标系,求线段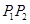 的中点且与
的中点且与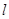 垂直的直线的极坐标方程.
垂直的直线的极坐标方程.
(本小题满分10分)选修1—4:几何证明选讲
如图,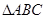 是直角三角形,
是直角三角形, .以
.以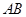 为直径的圆
为直径的圆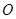 交
交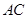 于点
于点 ,点
,点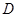 是
是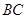 边的中点.连结
边的中点.连结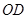 交圆
交圆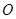 于点
于点 .
.
(Ⅰ)求证: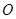 、
、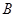 、
、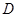 、
、 四点共圆;
四点共圆;
(Ⅱ)求证: