(本小题满分10分)选修4-4:坐标系与参数方程
将圆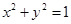 每一点的,横坐标保持不变,纵坐标变为原来的2倍,得到曲线C.
每一点的,横坐标保持不变,纵坐标变为原来的2倍,得到曲线C.
(Ⅰ)写出C的参数方程;
(Ⅱ)设直线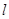 :
: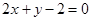 与C的交点为
与C的交点为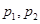 ,以坐标原点为极点,
,以坐标原点为极点,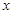 轴的正半轴为极轴建立极坐标系,求线段
轴的正半轴为极轴建立极坐标系,求线段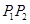 的中点且与
的中点且与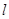 垂直的直线的极坐标方程.
垂直的直线的极坐标方程.
(本小题满分12分)
某研究机构为了研究人的体重与身高之间的关系,随机抽测了20人,得到如下 数据:
数据:
(1)若“身高大于175厘米”的为 “高个”,“身高小于等于175厘米”的为“非高个”;“体重大于75(公斤)”的为“胖子”,“体重小于等于75(公
“高个”,“身高小于等于175厘米”的为“非高个”;“体重大于75(公斤)”的为“胖子”,“体重小于等于75(公 斤)”的为“非胖子”.请根据上表数据完成下面的
斤)”的为“非胖子”.请根据上表数据完成下面的 联列表:
联列表:
| 高个 |
非高个 |
合计 |
|
| 胖 子 |
|||
| 非胖子 |
12 |
||
| 合计 |
20 |
(2)根据题(1)中表格的数据,若按99%的可靠性要求,能否认为体重与身高之间有关系?
(本小题满分12分)
下表是关于某设备的使用年限 (年)和所需要的维修费用
(年)和所需要的维修费用 (万元)的几组统计数据:
(万元)的几组统计数据:
 |
2 |
3 |
4 |
5 |
6 |
 |
2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
(1)请在给出的坐标系中画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出 关于
关于 的线性回归方程
的线性回归方程 ;
;
(3)估计使用年限为10年时,维修费用为 多少?
(参考数值: )
)
(本小题满分12分)
当实数 m为何值时,复数  (
( )在复平面内对应的点,
)在复平面内对应的点,
(1)在实轴上?
(2)在第四象限?
(3)位于 轴负半轴上?
轴负半轴上?
三、解答题. (本大题共6题,第17-21题每题12分,第22题14分)
17、(本小题满分12分)
某公司做人事调整:设总经理一个,配有经理助理一名;设副经理两人,直接对总经理负责,设有6个部门,其中副经理A管理生产部、安全部和质量部,经理B管理销售部、财务部和保卫部;生产车间由生产部和安全部共同管理,公司配有质检中心和门岗。请根据以上信息设计并画出该公司的人事结构图。
如图,在长方体 中,
中, ,
, ,点
,点 在棱
在棱 上移动,请用空间向量方法计算,
上移动,请用空间向量方法计算,
(1)当E为AB中点时,求直线DE与平面 所成角的余弦值
所成角的余弦值
(2)当 等于何值时,二面角
等于何值时,二面角 的大小为
的大小为 .
.