某中学一名数学老师对全班50名学生某次考试成绩分男女生进行了统计(满分150分),其中120分(含120分)以上为优秀,绘制了如下的两个频率分布直方图: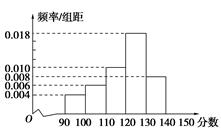
男生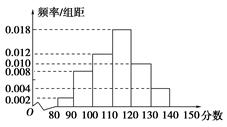
女生
(1)根据以上两个直方图完成下面的2×2列联表:
| 成绩性别 |
优秀 |
不优秀 |
总计 |
| 男生 |
|
|
|
| 女生 |
|
|
|
| 总计 |
|
|
|
(2)根据(1)中表格的数据计算,你有多大把握认为学生的数学成绩与性别之间有关系?
(注:
| k0 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
| P(K2≥k0) |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
K2= ,其中n=a+b+c+d.)
,其中n=a+b+c+d.)
(3)若从成绩在[130,140]的学生中任取2人,求取到的2人中至少有1名女生的概率.
如图,四棱锥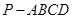 的底面是矩形,侧面
的底面是矩形,侧面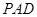 是正三角形,且侧面
是正三角形,且侧面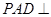 底面
底面 ,
,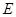 为侧棱
为侧棱 的中点.
的中点.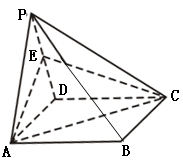
(1)求证: 平面
平面 ;
;
(2)若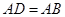 ,试求二面角
,试求二面角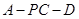 的余弦值.
的余弦值.
已知一几何体如图所示,正方形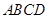 和梯形
和梯形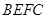 所在平面互相垂直,
所在平面互相垂直,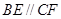 ,
, ,
,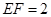 ,
,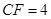 ,
,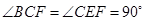 .
.
(Ⅰ)求证: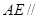 平面
平面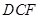 ;
;
(Ⅱ)求该几何体的体积.
如图,在四棱锥 中,底面
中,底面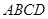 是菱形,
是菱形,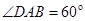 ,
, 平面
平面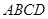 ,
, ,点
,点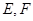 分别为
分别为 和
和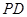 中点.求
中点.求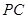 与平面
与平面 所成角的正弦值.
所成角的正弦值.
在平面直角坐标系中, 已知 的三个顶点的坐标分别是
的三个顶点的坐标分别是 .
.
(1)如果 是直角,求实数
是直角,求实数 的值;
的值;
(2)求过坐标原点,且与 的高
的高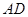 垂直的直线
垂直的直线 的方程.
的方程.
如图所示,在四棱锥P—ABCD中,底面ABCD是正方形,E、F分别为PC、BD的中点,平面PAD⊥平面ABCD,且PA=PD= AD.
AD.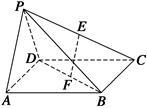
(1)求证:EF∥平面PAD;
(2)求证:平面PAB⊥平面PCD.