九（1）班数学兴趣小组经过市场调查，整理出某种商品在第x（1≤x≤90）天的售价与销售量的相关信息如下表：
| 时间x（天） |
1≤x＜50 |
50≤x≤90 |
| 售价（元/件） |
x＋40 |
90 |
| 每天销量（件） |
200－2x |
已知该商品的进价为每件30元，设销售该商品的每天利润为y元[
（1）求出y与x的函数关系式；
（2）问销售该商品第几天时，当天销售利润最大，最大利润是多少？
（3）该商品在销售过程中，共有多少天每天销售利润不低于4800元？请直接写出结果.
如图，大海中有A和B两个岛屿，为测量它们之间的距离，在海岸线PQ上点E处测得∠AEP=74°，∠BEQ=30°；在点F处测得∠AFP=60°，∠BFQ=60°，EF=1km．
（1）判断AB，AE的数量关系，并说明理由；
（2）求两个岛屿A和B之间的距离（结果精确到0.1km）．
（参考数据：
≈1.73，sin74°≈0.96，cos74°≈0.28，tan74°≈3.49，sin76°≈0.97，cos76°≈0.24，tan76°≈4.01）
在1个不透明的口袋里，装有红、白、黄三种颜色的乒乓球（除颜色外，其余都相同），其中有白球2个，黄球1个，若从中任意摸出一个球，这个球是白色的概率为0.5．
（1）求口袋中红球的个数；
（2）若摸到红球记0分，摸到白球记1分，摸到黄球记2分，甲从口袋中摸出一个球，不放回，再找出一个画树状图的方法求甲摸的两个球且得2分的概率．
解方程组：
．
如图，在Rt△ABC中，∠C=90°，∠ABC的平分线BD交AC于点D，DE⊥DB交AB于点E，设⊙O是△BDE的外接圆．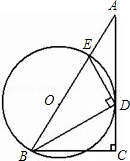
（1）求证：AC是⊙O的切线；
（2）若DE=2，BD=4，求AE的长．
先化简再求值
，已知a2+2a﹣7=0．