如图,Rt△ABC中,∠ACB=90°,AC=6 cm,BC=8 cm,动点P从点B出发,在BA边上以每秒5 cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4 cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
(1)若△BPQ与△ABC相似,求t的值;
(2)连接AQ、CP,若AQ⊥CP,求t的值;
(3)试证明:PQ的中点在△ABC的一条中位线上.
先化简,再求值 ,其中
,其中 ,
, .
.
因式分解:x2+3x(x-3)-9
计算题
(1)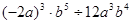
(2)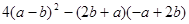
在数学探究课上,老师出示了这样的探究问题,请你一起来探究:已知:C是线段AB所在平面内任意一点,分别以AC、BC为边,在AB同侧作等边△ACE和△BCD,连结AD、BE交于点P.
(1)如图1,当点C在线段AB上移动时,线段AD 与BE的数量关系: .
(2)如图2,当点C在直线AB外,且∠ACB<120°,上面的结论是否还成立?若成立请证明,不成立说明理由.
(3)如图3,在(2)的条件下,以AB为边在AB另一侧作等边三角形△ABF,连结AD、BE和CF交于点P,求证:PB+PC+PA=BE.
已知:三角形ABC中,∠A=90°,AB=AC,D为BC的中点,
(1)如图①,E,F分别是AB,AC上的点,且BE=AF,求证:△DEF为等腰直角三角形.
(2)如图②,若E,F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,那么△DEF是否仍为等腰直角三角形?证明你的结论.