设 为奇函数,
为奇函数, 为常数.
为常数.
(1)求 的值;
的值;
(2)证明 在区间(1,+∞)内单调递增;
在区间(1,+∞)内单调递增;
(3)若对于区间[3,4]上的每一个 的值,不等式
的值,不等式 >
> 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
如图,四边形ABCD是正方形,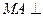 平面ABCD,MA//PB,PB=AB=2MA=2。
平面ABCD,MA//PB,PB=AB=2MA=2。
(1)P、C、D、M四点是否在同一平面内,为什么?
(2)求证:面PBD  面PAC;
面PAC;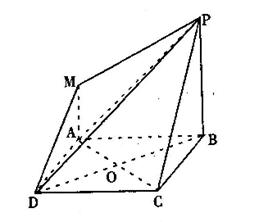 (3)求直线BD和平面PMD所成角的正弦值。
(3)求直线BD和平面PMD所成角的正弦值。
某市图书馆有三部电梯,每位乘客选择哪部电梯到阅览室的概率都是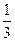 。现有5位乘客准备乘电梯到阅览室。
。现有5位乘客准备乘电梯到阅览室。
(1)求5位乘客选择乘同一部电梯到阅览室的概率;
(2)若记5位乘客中乘第一部电梯到阅览室的人数为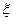 ,求
,求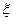 的分布列和数学期望
的分布列和数学期望
已知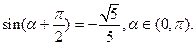 )
)
(1)求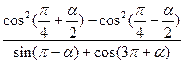 的值;
的值;
(2)求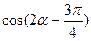 的值。
的值。
(本小题满分12分)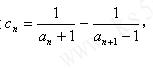
已知数列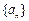 的前n项和
的前n项和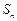 满足:
满足: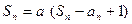 (
(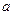 为常数,且
为常数,且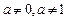 ).
).
(Ⅰ)求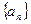 的通项公式;
的通项公式;
(Ⅱ)设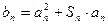 ,若数列
,若数列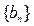 为等比数列,求
为等比数列,求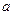 的值;
的值;
(Ⅲ)在满足条件(Ⅱ)的情形下,设,数列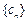 的前n项和为
的前n项和为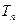 .求证:
.求证: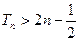 .
.
(本小题满分12分)设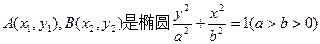 上的两点,已知向量
上的两点,已知向量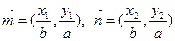 ,若
,若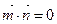 且椭圆的离心率e=,短轴长为
且椭圆的离心率e=,短轴长为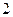 ,
,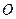 为坐标原点.
为坐标原点.
(Ⅰ)求椭圆的方程;
(Ⅱ)试问:△AOB的面积是否为定值?如果是,请给予证明;如果不是,请说明理由