设椭圆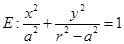 的焦点在
的焦点在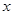 轴上,
轴上, 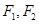 分别是椭圆的左、右焦点,点
分别是椭圆的左、右焦点,点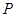 是椭圆在第一象限内的点,直线
是椭圆在第一象限内的点,直线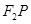 交
交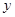 轴于点
轴于点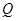 ,
,
(1)当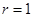 时,
时,
(1)若椭圆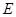 的离心率为
的离心率为 ,求椭圆
,求椭圆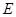 的方程;
的方程;
(2)当点P在直线 上时,求直线
上时,求直线 与
与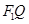 的夹角;
的夹角;
(2) 当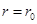 时,若总有
时,若总有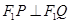 ,猜想:当
,猜想:当 变化时,点
变化时,点 是否在某定直线上,若是写出该直线方程(不必求解过程).
是否在某定直线上,若是写出该直线方程(不必求解过程).
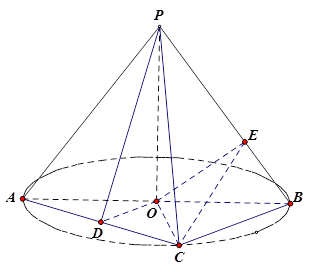
【2015高考福建,文20】如图, 是圆
是圆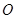 的直径,点
的直径,点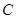 是圆
是圆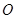 上异于
上异于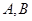 的点,
的点, 垂直于圆
垂直于圆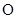 所在的平面,且
所在的平面,且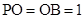 .
.
(Ⅰ)若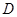 为线段
为线段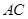 的中点,求证
的中点,求证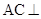 平面
平面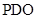 ;
;
(Ⅱ)求三棱锥 体积的最大值;
体积的最大值;
(Ⅲ)若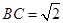 ,点
,点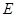 在线段
在线段 上,求
上,求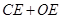 的最小值.
的最小值.
【2015高考北京,文18】(本小题满分14分)如图,在三棱锥 中,平面
中,平面 平面
平面 ,
, 为等边三角形,
为等边三角形, 且
且 ,
, ,
, 分别为
分别为 ,
,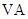 的中点.
的中点.
(Ⅰ)求证: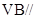 平面
平面 ;
;
(Ⅱ)求证:平面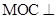 平面
平面 ;
;
(Ⅲ)求三棱锥 的体积.
的体积.
【2015高考安徽,文19】如图,三棱锥P-ABC中,PA 平面ABC,
平面ABC, .
.
(Ⅰ)求三棱锥P-ABC的体积;
(Ⅱ)证明:在线段PC上存在点M,使得AC BM,并求
BM,并求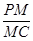 的值.
的值.
【2015高考上海,文22】本题共3个小题,第1小题4分,第2小题6分,第3小题6分.
已知椭圆 ,过原点的两条直线
,过原点的两条直线 和
和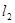 分别于椭圆交于
分别于椭圆交于 、
、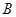 和
和 、
、 ,设
,设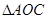 的面积为
的面积为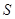 .
.
(1)设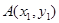 ,
,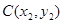 ,用
,用 、
、 的坐标表示点
的坐标表示点 到直线
到直线 的距离,并证明
的距离,并证明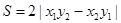 ;
;
(2)设 ,
,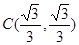 ,
,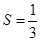 ,求
,求 的值;
的值;
(3)设 与
与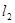 的斜率之积为
的斜率之积为 ,求
,求 的值,使得无论
的值,使得无论 与
与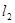 如何变动,面积
如何变动,面积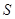 保持不变.
保持不变.
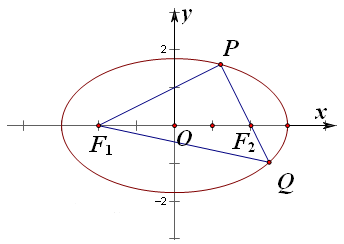
【2015高考重庆,文21】如图,椭圆 (
(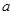 >
> >0)的左右焦点分别为
>0)的左右焦点分别为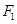 ,
, ,且过
,且过 的直线交椭圆于P,Q两点,且PQ
的直线交椭圆于P,Q两点,且PQ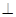
 .
.
(Ⅰ)若| |=2+
|=2+ ,|
,| |=2-
|=2- ,求椭圆的标准方程.
,求椭圆的标准方程.
(Ⅱ)若|PQ|=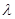 |
| |,且
|,且
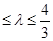 ,试确定椭圆离心率的取值范围.
,试确定椭圆离心率的取值范围.