如图,椭圆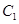 :
: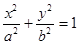 (
(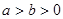 )和圆
)和圆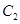 :
: ,已知圆
,已知圆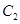 将椭圆
将椭圆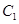 的长轴三等分,且
的长轴三等分,且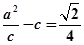 ,椭圆
,椭圆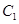 的下顶点为
的下顶点为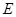 ,过坐标原点
,过坐标原点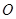 且与坐标轴不重合的任意直线
且与坐标轴不重合的任意直线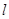 与圆
与圆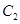 相交于点
相交于点 、
、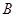 .
.
(1)求椭圆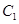 的方程;
的方程;
(2)若直线 、
、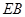 分别与椭圆
分别与椭圆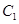 相交于另一个交点为点
相交于另一个交点为点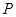 、
、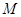 .
.
①求证:直线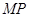 经过一定点;
经过一定点;
|
②试问:是否存在以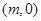 为圆心,
为圆心, 为半径的圆
为半径的圆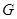 ,使得直线
,使得直线 和直线
和直线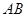 都与圆
都与圆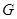 相交?若存在,请求出所有
相交?若存在,请求出所有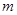 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

((本小题满分10分)选修4—4:坐标系与参数方程
已知极坐标系的极点是直角坐标系的原点,极轴与直角坐标系中 轴的正半轴重合.曲线
轴的正半轴重合.曲线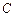 的极坐标方程为
的极坐标方程为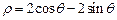 ,曲线
,曲线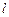 的极坐标方程是
的极坐标方程是 .
.
(Ⅰ)求曲线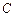 和
和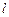 的直角坐标方程并画出草图;
的直角坐标方程并画出草图;
(Ⅱ)设曲线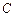 和
和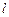 相交于
相交于 ,
, 两点,求
两点,求 .
.
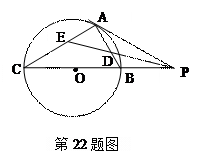
(本小题满分10分)选修4—1:几何证明选讲
如图,已知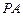 与圆
与圆 相切于点
相切于点 ,经过点
,经过点 的割线
的割线 交圆
交圆 于点
于点 ,
, 的平分线分别交
的平分线分别交 于点
于点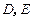 .
.
(Ⅰ)证明: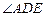 =
= ;
;
(Ⅱ)若 ,求
,求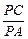 的值.
的值.
((本小题满分12分)
已知函数 .
.
(Ⅰ)若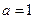 ,求曲线
,求曲线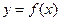 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)若函数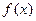 在其定义域内为增函数,求
在其定义域内为增函数,求 的取值范围;
的取值范围;
(Ⅲ)设函数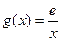 ,若在
,若在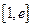 上至少存在一点
上至少存在一点 ,使得
,使得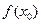
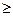
 成立,求实数
成立,求实数 的取值范围.
的取值范围.
((本小题满分12分)
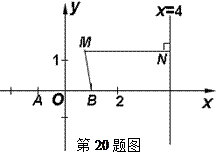
如图,已知两定点 ,
, 和定直线
和定直线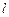 :
: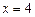 ,动点
,动点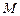 在直线
在直线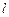 上的射影为
上的射影为 ,且
,且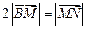 .
.
(Ⅰ)求动点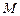 的轨迹
的轨迹 的方程并画草图;
的方程并画草图;
(Ⅱ)是否存在过点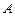 的直线
的直线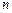 ,使得直线
,使得直线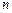 与曲线
与曲线 相交于
相交于 ,
,  两点,且△
两点,且△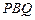 的面积等于
的面积等于 ?如果存在,请求出直线
?如果存在,请求出直线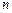 的方程;如果不存在,请说明理由.
的方程;如果不存在,请说明理由.
((本小题满分12分)
如图,已知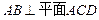 ,
,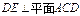 ,
,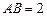 ,
,
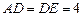 ,
, .
.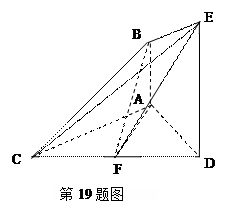
(Ⅰ)求证:
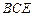 ;
;
(Ⅱ) 若 ,求二面角
,求二面角 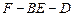 的余弦值.
的余弦值.