已知函数 .
.
(1)若函数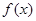 在
在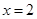 时取得极值,求实数
时取得极值,求实数 的值;
的值;
(2)若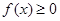 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分14分)
已知函数 ,
, ,它们的定义域都是
,它们的定义域都是 ,其中
,其中 ,
,
(Ⅰ)当 时,求函数
时,求函数 的单调区间;
的单调区间;
(Ⅱ)当 时,对任意
时,对任意 ,求证:
,求证:
(Ⅲ)令 ,问是否存在实数
,问是否存在实数 使得
使得 的最小值是3,如果存在,求出
的最小值是3,如果存在,求出 的值;如果不存在,说明理由。
的值;如果不存在,说明理由。
(本小题满分14分)
一种计算装置,有一数据入口点A和一个运算出口点B ,按照某种运算程序:
①当从A口输入自然数1时,从B口得到 ,记为
,记为 ;
;
② 当从A口输入自然数
当从A口输入自然数 时,在B口得到的结果
时,在B口得到的结果 是前一个结果
是前一个结果 的
的 倍;
倍;
试问:当从A口分别输入自然数2 ,3 ,4 时,从B口分别得到什么数?试猜想 的关系式,并证明你的结论。
的关系式,并证明你的结论。
(本小题满分13分)
已知函数 在
在 与
与 处都取得极值。
处都取得极值。
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)求函数 在区间[-2,2]的最大值与最小值。
在区间[-2,2]的最大值与最小值。
(本小题满分13分)
已知命题:平面上一矩形ABCD的对角线AC与边AB、AD所成的角分别为 、
、 (如图1),则
(如图1),则 .用类比的方法,把它推广到空间长方体中,试写出相应的一个真命题并证明。
.用类比的方法,把它推广到空间长方体中,试写出相应的一个真命题并证明。

甲、乙两人各进行3次射击,甲每次击中目标的概率为 ,乙每次击中目标的概率
,乙每次击中目标的概率 ,
,
(I)记甲击中目标的次数为X,求X的概率分布及数学期望;
(Ⅱ)求甲恰好比乙多击中目标2次的概率。